Advertisements
Advertisements
Question
Derive the expression for the terminal velocity of a sphere moving in a high viscous fluid using stokes force.
Solution
Expression for terminal velocity: Consider a sphere of radius r which falls freely through a highly viscous liquid of coefficient of viscosity η. Let the density of the material of the sphere be ρ and the density of the fluid be σ.
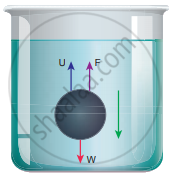
Forces acting on the sphere when it falls in a viscous liquid
Gravitational force acting on the sphere,
FG = mg = `4/3π"r"^3ρ"g"` (downward force)
Upthrust, U = `4/3π"r"^3σ"g"` (upward force)
Viscous force, F = 6πηrvt
At terminal velocity vt,
Downward force = upward force
FG = U + F
FG − U = F ⇒ `4/3π"r"^3ρ"g" - 4/3π"r"^3σ"g"` = 6πηrvt
vt = `2/9 xx ("r"^2(ρ - σ))/η` g ⇒ `"v"_"t" ∝ "r"^2`
Here, it should be noted that the terminal speed of the sphere is directly proportional to the square of its radius. If a is greater than ρ, then the term (ρ – σ) becomes negative leading to a negative terminal velocity.
APPEARS IN
RELATED QUESTIONS
Explain why The size of the needle of a syringe controls flow rate better than the thumb pressure exerted by a doctor while administering an injection
In Millikan’s oil drop experiment, what is the terminal speed of an uncharged drop of radius 2.0 × 10–5 m and density 1.2 × 103 kg m–3? Take the viscosity of air at the temperature of the experiment to be 1.8 × 10–5 Pa s. How much is the viscous force on the drop at that speed? Neglect buoyancy of the drop due to air.
A metal sphere of radius 1 mm and mass 50 mg falls vertically in glycerine. Find (a) the viscous force exerted by the glycerine on the sphere when the speed of the sphere is 1 cm s−1, (b) the hydrostatic force exerted by the glycerine on the sphere and (c) the terminal velocity with which the sphere will move down without acceleration. Density of glycerine = 1260 kg m−3 and its coefficient of viscosity at room temperature = 8.0 poise.
Estimate the speed of vertically falling raindrops from the following data. Radius of the drops = 0.02 cm, viscosity of air = 1.8 × 10−4 poise, g= 9.9 × 10 ms−2 and density of water = 1000 kg m−3.
The unit of viscosity is
Which has greater viscosity, oil or honey? Why?
Derive Poiseuille’s formula for the volume of a liquid flowing per second through a pipe under streamlined flow.
From amongst the following curves, which one shows the variation of the velocity v with time t for a small-sized spherical body falling vertically in a long column of a viscous liquid.
The velocity of a small ball of mass M and density d, when dropped in a container filled with glycerine becomes constant after some time. If the density of glycerine is `"d"/2`, then the viscous force acting on the ball will be ______
An air bubble of negligible weight having radius r rises steadily through a solution of density σ at speed v. The coefficient of viscosity of the solution is given by ______.
