Advertisements
Advertisements
Question
दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।
निम्न अवरोधों के अंतर्गत Z = x + y का अधिकतमीकरण कीजिए:
x - y ≤ -1, -x + y ≤ 0, x, y ≥ 0.
Solution
बाधाओं की प्रणाली इस प्रकार है:
x - y ≤ -1 ....(i)
- x + y ≤ 0 ....(ii)
x, y ≥ 0 ....(iii)
माना l1 : x - y = -1
l2 : -x + y = 0
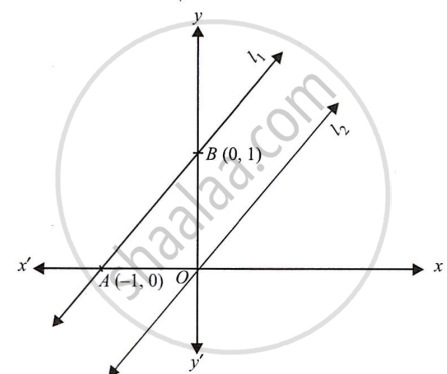
यह क्षेत्र बंधित नहीं है और ना ही कोई क्षेत्र समान है अतः Z अधिकतम मात्रा संभव नहीं है।
APPEARS IN
RELATED QUESTIONS
ग्राफ़ीय विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए:
निम्न अवरोधों के अंतर्गत Z = 5x + 3y का अधिकतमीकरण कीजिए:
3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
ग्राफ़ीय विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए:
निम्न अवरोधों के अंतर्गत Z = 3x + 5y का न्यूनतमीकरण कीजिए:
x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0
ग्राफ़ीय विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए:
निम्न अवरोधों के अंतर्गत Z = 3x + 2y का न्यूनतमीकरण कीजिए:
x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0
ग्राफ़ीय विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए:
निम्न अवरोधों के अंतर्गत Z = x + 2y का न्यूनतमीकरण कीजिए:
2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0
दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।
निम्न अवरोधों के अंतर्गत Z = 5x + 10y का न्यूनतमीकरण तथा अधिकतमीकरण कीजिए:
x + 2y ≤ 120, x + y ≥ 60, x - 2y ≥ 0, x, y ≥ 0.
दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।
निम्न अवरोधों के अंतर्गत Z = x + 2y का न्यूनतमीकरण तथा अधिकतमीकरण कीजिए:
x + 2y ≥ 100, 2x - y ≤ 0, 2x + y ≤ 200; x, y ≥ 0.
दिखाइए कि Z का न्यूनतम मान दो बिंदुओं से अधिक बिंदुओं पर घटित होता है।
निम्न अवरोधों के अंतर्गत Z = -x + 2y का अधिकतमीकरण कीजिए:
x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
