Advertisements
Advertisements
Question
दिलेल्या आकृतीत AP ⊥ BC, AD || BC, तर A(Δ ABC) : A(Δ BCD) काढा.
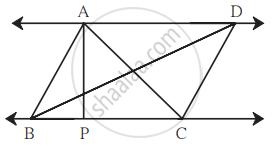
Solution
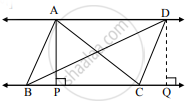
DQ ⊥ BC काढा. B-C-Q
AD || BC ........ [पक्ष]
∴ AP = DQ ........ (i) [दोन समांतर रेषेतील लंबउंची समान असते.]
ΔABC आणि ΔBCD चा BC हा सामाईक पाया आहे.
`"A(ΔABC)"/"A(ΔBCD)" = "AP"/"DQ"` .......... [समान पाया असलेले त्रिकोण]
= `"AP"/"AP"` ........... [(i) वरून]
= 1
∴ A(ΔABC) : A(ΔBCD) = 1 : 1
APPEARS IN
RELATED QUESTIONS
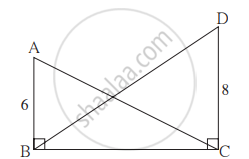
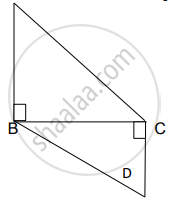
आकृती मध्ये ∠ABC = ∠DCB = 90° AB = 6, DC = 8 तर `("A"(Δ"ABC"))/("A"(Δ"DCB"))` = किती?
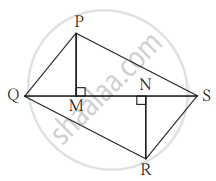
आकृती मध्ये PM = 10 सेमी A(ΔPQS) = 100 चौसेमी A(ΔQRS) = 110 चौसेमी तर NR काढा.
जर ∆XYZ ~ ∆PQR, तर `"XY"/"PQ" = "YZ"/"QR"` = ?
∆PQR ~ ∆SUV, तर त्या त्रिकोणाच्या एकरूप कोनांच्या जोड्या लिहा.
∆ABC ~ ∆DEF, तर प्रमाणात असणाऱ्या संगत बाजू लिहा.
आकृतीमध्ये, AB लंब BC आणि DC लंब BC, AB = 6, DC = 4, तर `("A"(Delta"ABC"))/("A"(Delta"BCD"))` = ?
त्रिकोणाच्या एका बाजूला समांतर असणारी रेषा त्याच्या उरलेल्या बाजूंना भिन्न बिंदूत छेदत असेल, तर ती रेषा त्या बाजूंना एकाच प्रमाणात विभागते. सिद्धता पूर्ण करा.
पक्ष: ∆ABC मध्ये रेषा l || बाजू BC आणि रेषा l ही बाजू AB ला P मध्ये व बाजू AC ला Q मध्ये छेदते.
साध्य: `"AP"/"PB" = "AQ"/"QC"`
रचना: रेख CP व रेख BQ काढा.
सिद्धता:
∆APQ व ∆PQB हे समान उंचीचे त्रिकोण आहेत.
`("A"(Delta"APQ"))/("A"(Delta"PQB")` = `square/"PB"` ..........[क्षेत्रफळे पायांच्या प्रमाणात] (i)
`("A"(Delta"APQ"))/("A"(Delta"PQC")` = `square/"QC"` ..........[क्षेत्रफळे पायांच्या प्रमाणात] (ii)
∆PQC व ∆PQB यांचा रेख `square` हा समान पाया आहे.
रेख PQ || रेख BC म्हणून: ∆∆APQ व ∆PQB यांची उंची समान आहे.
A(∆PQC) = A(∆ `square`) ........….(iii)
`("A"(Delta"APQ"))/("A"(Delta"PQB")` = `("A"(∆ square))/("A"(∆ square))` ..............[(i), (ii) व (iii]
`"AP"/"PB" = "AQ"/"QC"` ......….[(i) व (ii) वरून]

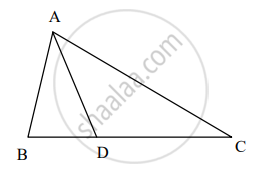
∆ABC मध्ये, B-D-C आणि BD = 7, BC = 20, तर खालील गुणोत्तर काढा.
`("A"(Delta"ABD"))/("A"(Delta"ADC"))`
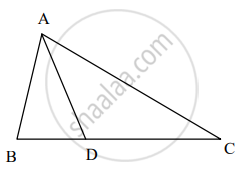
∆ABC मध्ये, B-D-C आणि BD = 7, BC = 20, तर खालील गुणोत्तर काढा.

`(A(∆ABD))/(A(∆ABC))`
∆ABC मध्ये, B-D-C आणि BD = 7, BC = 20, तर खालील गुणोत्तर काढा.
`("A"(Delta"ADC"))/("A"(Delta"ABC"))`