Advertisements
Advertisements
Question
Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords. Where do they meet?
Solution
-
Mark any point C on the sheet. Now, by adjusting the compasses up to 4 cm and by putting the pointer of compasses at point C, turn the compasses slowly to draw the circle. It is the required circle of 4 cm radius.

- Take any two chords `overline"AB"` and `overline"CD"` in the circle.
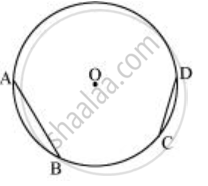
- Taking A and B as centres and with radius more than half of `overline"AB"`, draw arcs on both sides of AB, intersecting each other at E, F. Join EF which is the perpendicular bisector of AB.
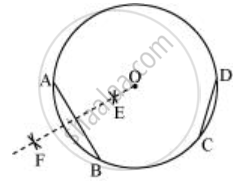
- Taking C and D as centres and with radius more than half of `overline"CD"`, draw arcs on both sides of CD, intersecting each other at G, H. Join GH which is the perpendicular bisector of CD.
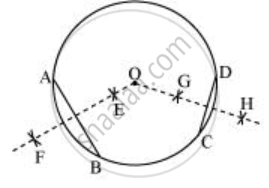
Now, we will find that when EF and GH are extended, they meet at the centre of the circle i.e., point O.
APPEARS IN
RELATED QUESTIONS
Draw a line segment PQ = 4.8 cm. Construct the perpendicular bisector of PQ.
Draw a line segment AB = 5.5 cm. Mark a point P, such that PA = 6 cm and PB = 4.8 cm. From point P, draw a perpendicular to AB.
Draw a line segment of given length and construct a perpendicular bisector to line segment using scale and compass
7 cm
Draw a line segment of given length and construct a perpendicular bisector to line segment using scale and compass
5.6 cm
Draw a line segment of given length and construct a perpendicular bisector to line segment using scale and compass
10.4 cm
Draw a line segment of given length and construct a perpendicular bisector to line segment using scale and compass
58 mm
It is possible to draw two bisectors of a given angle.
Draw a line segment of length 7 cm. Draw its perpendicular bisector, using ruler and compasses.
Copy figure on your notebook and draw a perpendicular from P to line m using (i) set squares (ii) protractor (iii) ruler and compass. How many such perpendicular are you able to draw?
Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement.
