Advertisements
Advertisements
प्रश्न
Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords. Where do they meet?
उत्तर
-
Mark any point C on the sheet. Now, by adjusting the compasses up to 4 cm and by putting the pointer of compasses at point C, turn the compasses slowly to draw the circle. It is the required circle of 4 cm radius.

- Take any two chords `overline"AB"` and `overline"CD"` in the circle.
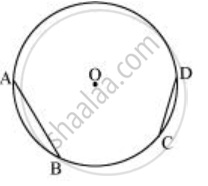
- Taking A and B as centres and with radius more than half of `overline"AB"`, draw arcs on both sides of AB, intersecting each other at E, F. Join EF which is the perpendicular bisector of AB.
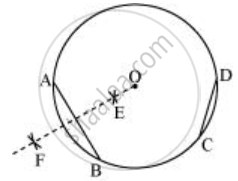
- Taking C and D as centres and with radius more than half of `overline"CD"`, draw arcs on both sides of CD, intersecting each other at G, H. Join GH which is the perpendicular bisector of CD.
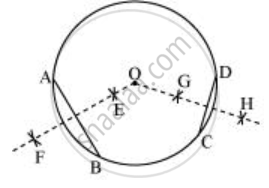
Now, we will find that when EF and GH are extended, they meet at the centre of the circle i.e., point O.
APPEARS IN
संबंधित प्रश्न
Draw a line segment AB = 5.5 cm. Mark a point P, such that PA = 6 cm and PB = 4.8 cm. From point P, draw a perpendicular to AB.
Draw a line segment AB of length 5.5 cm. Bisect it using a compass and ruler.
Draw a line segment of given length and construct a perpendicular bisector to line segment using scale and compass
5.6 cm
It is possible to draw two bisectors of a given angle.
Infinitely many perpendiculars can be drawn to a given ray.
Infinitely many perpendicular bisectors can be drawn to a given ray.
In figure, the point C is the image of point A in line l and line segment BC intersects the line l at P.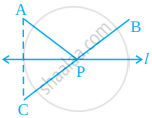
(a) Is the image of P in line l the point P itself?
(b) Is PA = PC?
(c) Is PA + PB = PC + PB?
(d) Is P that point on line l from which the sum of the distances of points A and B is minimum?
Bisect ∠XYZ of figure.
Bisect a straight angle, using ruler and compasses. Measure each part.
Draw any angle with vertex O. Take a point A on one of its arms and B on another such that OA = OB. Draw the perpendicular bisectors of `overline"OA"` and `overline"OB"`. Let them meet at P. Is PA = PB ?
