Advertisements
Advertisements
प्रश्न
Draw any angle with vertex O. Take a point A on one of its arms and B on another such that OA = OB. Draw the perpendicular bisectors of `overline"OA"` and `overline"OB"`. Let them meet at P. Is PA = PB ?
उत्तर
- Draw any angle whose vertex is O.
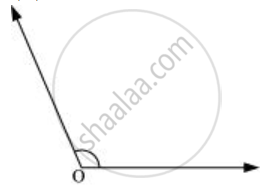
- With a convenient radius, draw arcs on both rays of this angle while taking O as centre. Let these points be A and B.
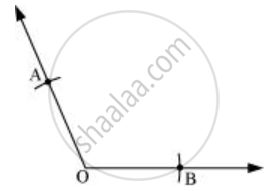
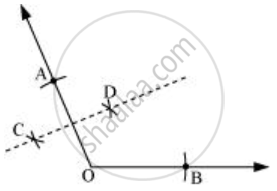
- Taking O and A as centres and with radius more than half of OA, draw arcs on both sides of OA. Let these be intersecting at C and D. Join CD.
-
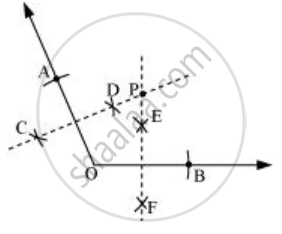
Similarly, we can find the perpendicular bisector `overline"EF"` of `overline"OB"`. These perpendicular bisectors `overline"CD"` and `overline"EF"` will intersect each other at P.
Now, PA and PB can be measured. These are equal in length.
APPEARS IN
संबंधित प्रश्न
Draw a line segment PQ = 4.8 cm. Construct the perpendicular bisector of PQ.
In each of the following, draw perpendicular through point P to the line segment AB :
(i)

(ii)

(iii)
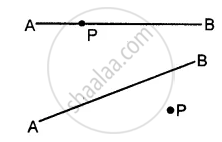
Draw a line segment AB = 5.5 cm. Mark a point P, such that PA = 6 cm and PB = 4.8 cm. From point P, draw a perpendicular to AB.
Draw a line segment of given length and construct a perpendicular bisector to line segment using scale and compass
8 cm
Draw a line segment of given length and construct a perpendicular bisector to line segment using scale and compass
7 cm
Draw a line segment of given length and construct a perpendicular bisector to line segment using scale and compass
5.6 cm
Draw a line segment of given length and construct a perpendicular bisector to line segment using scale and compass
58 mm
Draw a line segment of length 6.5 cm and divide it into four equal parts, using ruler and compasses.
Bisect a straight angle, using ruler and compasses. Measure each part.
Draw a line segment of length 9.5 cm and construct its perpendicular bisector.
