Advertisements
Advertisements
Question
The initial pressure and volume of a gas enclosed in a cylinder are 2 × 105 N/m2 and 6 × 10-3 m3 respectively. If the work done in compressing the gas at constant pressure is 150 J. find the final volume of the gas.
Solution
Given data,
ρ = 2 × 105 N/m2
Vi = 6 × 10-3
W = - 150 J
Vf = ?
W = P(Vf - Vi)
Vf = Vi + `"W"/"P"`
`= 6 xx 10^-3 + ((- 150)/(2 xx 10^5))`
`= 6 xx 10^-3 + (- 75 xx 10^-5)`
`= 6 xx 10^-3 - 0.75 xx 10^-3`
`"V"_"f" = 5.25 xx 10^-3 "m"^3`
Flnal volume of the gas is 5.25 × 10-3 m3.
APPEARS IN
RELATED QUESTIONS
Draw a neat and labelled diagram of suspended coil type moving coil galvanometer.
Write the expression for the magnetic moment `vecm`due to a planar square loop of side ‘l’ carrying a steady current I in a vector form.
In the given figure this loop is placed in a horizontal plane near a long straight conductor carrying a steady current I1 at a distance l as shown. Give reason to explain that the loop will experience a net force but no torque. Write the expression for this force acting on the loop.

Will a current loop placed in a magnetic field always experience a zero force?
Is it possible for a current loop to stay without rotating in a uniform magnetic field? If yes, what should be the orientation of the loop?
The torque on a current loop is zero if the angle between the positive normal and the magnetic field is either θ = 0 or θ = 180°. In which of the two orientations, the equilibrium is stable?
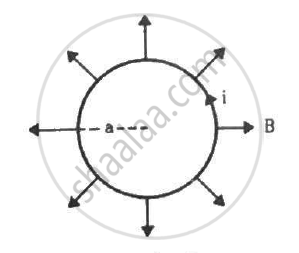
A circular loop of radius a, carrying a current i, is placed in a two-dimensional magnetic field. The centre of the loop coincides with the centre of the field (figure). The strength of the magnetic field at the periphery of the loop is B. Find the magnetic force on the wire.
A current loop of arbitrary shape lies in a uniform magnetic field B. Show that the net magnetic force acting on the loop is zero.
The figure shows a circular wire loop of radius a and carrying a current i, which is placed in a perpendicular magnetic field B. (a) Consider a small part dl of the wire. Find the force on this part of the wire exerted by the magnetic field. (b) Find the force of compression in the wire.
A circular loop of one turn carries a current of 5.00 A. If the magnetic field B at the centre is 0.200 mT, find the radius of the loop.
A moving coil galvanometer has been fitted with a rectangular coil having 50 turns and dimensions 5 cm × 3 cm. The radial magnetic field in which the coil is suspended is of 0.05 Wb/m2. The torsional constant of the spring is 1.5 × 10−9 Nm/degree. Obtain the current required to be passed through the galvanometer so as to produce a deflection of 30°.
A Rectangular coil of 10 turns, each of area 0.05 m2, is suspended freely in a uniform magnetic field of induction 0.01 T. A current of 30 µA is passed through it.
(i) What is the magnetic moment of the coil?
(ii) What is the maximum torque experienced by the coil?
The `(tau - theta)` graph for a coil is
A small cylindrical soft iron piece is kept in a galvanometer so that
If number of turns in moving coil galvanometer becomes half, then the deflection for the same current will become ____________.
The magnetic field developed due to current carrying coil at its centre is 'B'. If the new coil of two turns is prepared from the above coil and same current is passed, then the magnetic field at the centre of the new coil will be ____________.
What is the magnetic moment of a current-carrying circular coil if the radius of the circular coil is 'R' and magnetic induction at the center is 'B'?
A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the
(a) total torque on the coil,
(b) total force on the coil,
(c) average force on each electron in the coil due to the magnetic field?
(The coil is made of copper wire of cross-sectional area 10–5 m2, and the free electron density in copper is given to be about 1029 m–3.)
When the plane of the coil is parallel to the field, torque will be ______
Equal current i flows in two segments of a circular loop in the direction shown in figure. Radius of the loop is r. The magnitude of magnetic field induction at the centre of the loop is ______.
A thin flexible wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is ______.


A rectangular coil of 10 turns, each of area 0.05 m2, is suspended freely in a radial magnetic field of 0.01 T. If the torsional constant of the suspension fibre is 5 × 10−9 N·m per degree, find the angle through which the coil rotates when a current of 30 μA is passed through it.
A circular coil having N turns of radius R carrying a current I is used to produce a magnetic field B at its centre O.
If this coil is opened and rewound such that the radius of the newly formed coil is 2R, carrying the same current I, what will be the magnetic field at the centre O?
An electron moving along positive X axis with a velocity of 8 ×107ms-1 enters a region having uniform magnetic field B = 1.3 × 10-3 T along positive Y axis.
- Explain why the electron describes a circular path.
- Calculate the radius of the circular path described by the electron.
