Advertisements
Advertisements
Question
Draw graphs of displacement, velocity, and acceleration against phase angle, for a particle performing linear S.H.M. from
- the mean position
- the positive extreme position.
Deduce your conclusions from the graph.
Solution
(a) Particle executing S.H.M., starting from mean position, towards positive:
Consider a particle performing S.H.M., with amplitude A and period T = 2π/ω starting from the mean position towards the positive extreme position where w is the angular frequency. Its displacement from the mean position (x), velocity (v), and acceleration (a) at any instant are
x = A sin ωt = A sin ωt
v = `"dx"/"dt"` = Aω cos ωt
a = `"dv"/"dt"` = − Aω2 sin ωt
Using these expressions, the values of x, v, and a at the end of every quarter of a period, starting from t = 0, are tabulated below.
| t | 0 | `"T"/4` | `"T"/2` | `"3T"/4` | T | `"5T"/4` |
| ωt | 0 | `π/2` | π | `"3π"/2` | 2π | `(5pi)/2` |
| x | 0 | A | 0 | −A | 0 | A |
| v | Aω | 0 | −Aω | 0 | Aω | 0 |
| a | 0 | −Aω2 | 0 | Aω2 | 0 | -Aω2 |
Using the values in the table we can plot graphs of displacement, velocity, and acceleration with time.
| (a) | 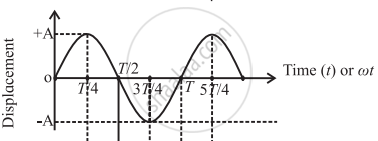 |
| (b) |  |
| (c) | 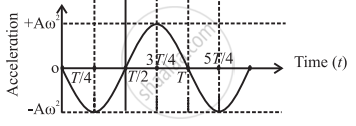 |
Graphs of displacement, velocity, and acceleration with time for a particle in SHM starting from the mean position
Conclusions:
- Displacement, velocity and acceleration of S.H.M. are periodic functions of time.
- Displacement time curve and acceleration time curves are sine curves and velocity time curve is a cosine curve.
- There is a phase difference of `π/2` radian between displacement and velocity.
- There is a phase difference of `π/2` radian between velocity and acceleration.
- There is a phase difference of π radian between displacement and acceleration.
- Shapes of all the curves get repeated after `2pi` radian or after a time T.
(b) Particle performing S.H.M., starting from the positive extreme position.
As the particle starts from the positive extreme position `phi = pi/2`
∴ Displacement, x = `A sin (omega"t" + pi/2) = A cos omega "t"`
∴ Velocity, v = `"dx"/"dt" = ("d"("A" cos omega"t"))/"dt" = - A omega sin (omega "t")`
∴ Acceleration,
a = `"dv"/"dt" = ("d"(- "A"omega sin (omega "t")))/"dt" = - Aomega^2 cos (omega "t")`
| t | 0 | `"T"/4` | `"T"/2` | `"3T"/4` | T | `"5T"/4` |
| θ | `pi/2` | π | `"3π"/2` | `"2π"` | `(5π)/2` | `3pi` |
| x | A | 0 | -A | 0 | A | 0 |
| v | 0 | - Aω | 0 | Aω | 0 | - Aω |
| a | - Aω2 | 0 | Aω2 | 0 | - Aω2 | 0 |
[Phase θ = ωt + `phi`]
| (a) |  |
| (b) | 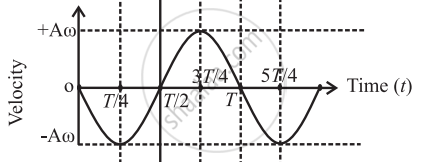 |
| (c) | 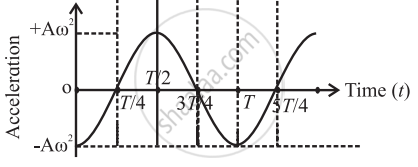 |
Conclusion -
- The displacement, velocity and acceleration of a particle performing linear SHM are periodic (harmonic) functions of time. For a particle starting from an extreme position, the x-t and a-t graphs are cosine curves; the v-t graph is a sine curve.
- There is a phase difference of `π/2` radians between x and v, and between v and a.
- There is a phase difference of n radians between x and a.
APPEARS IN
RELATED QUESTIONS
The amplitude and the periodic time of an S.H.M are 5 cm and 6 s respectively. At a distance of 2.5 cm from the mean position, the phase will be:
A particle executing SHM has velocities v1 and v2 at distances x1 and x2 respectively, from the mean position. Its time period is ______.
