Question

Show that a linear S.H.M. is the projection of a U.C.M. along any of its diameter.

Answer 1

Linear S.H.M. is defined as the linear periodic motion of a body in which the restoring force (or acceleration) is always directed towards the mean position, and its magnitude is directly proportional to the displacement from the mean position.
There is a basic relation between S.H.M. and U.C.M. that is very useful in understanding S.H.M. For an object performing U.C.M., the projection of its motion along any diameter of its path executes S.H.M.
Consider particle ‘P’ is moving along the circumference of a circle of radius ‘a’ with a constant angular speed of ω in an anticlockwise direction, as shown in the figure.
Particle P along the circumference of the circle has its projection particle on diameter AB at point M. Particle P is called a reference particle, and in the circle on which it moves, its projection moves back and forth along the horizontal diameter, AB.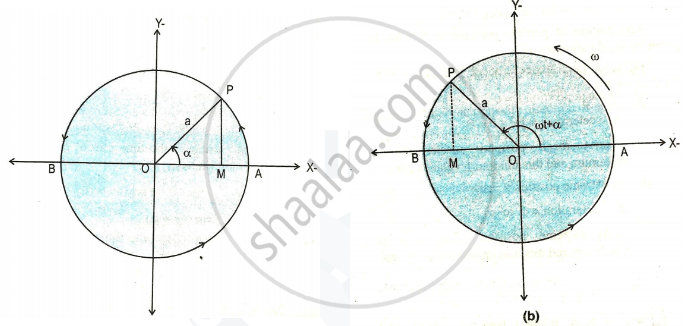

The x-component of the displacement of P is always the same as the displacement of M, the x-component of the velocity of P is always the same as the velocity of M and the x-component of the acceleration of M.
Suppose that particle P starts from the initial position with initial phase α (angle between radius OP and the x-axis at the time t = 0). In time t, the angle between OP and x-aaxis is ( ωt + α ) as particle P moving with constant angular velocity (ω) as shown in figure.
cos( ωt + α ) = `x/a`

`therefore x=acos(omegat+alpha)`                       ......(1)

This is the expression for displacement of particle M at time t.
As the velocity of the particle is the time rate of change of displacement, then we have

`v=dx/dt=d/dt[acos(omegat+alpha)]`

`therefore v=-a omega sin(omegat+alpha)`            ......(2)

As the acceleration of a particle is the time rate of change of velocity, we have

`a=(dv)/dt=d/dt [-a omega sin(omegat+alpha)]`

`therefore  a=-aomega^2cos(omegat+alpha)`

`therefore  a= -omega^2x`

It shows that the acceleration of particle M is directly proportional to its displacement, and its direction is opposite to that of displacement. Thus, particle M performs simple harmonic motion, but M is a projection of the particle performing U.C.M.; hence, S.H.M. is a projection of U.C.M. along the diameter of the circle.