Advertisements
Advertisements
Question
Draw a histogram for the following distribution and estimate the mode:
| I.Q. Score | 80-100 | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 |
| No. of Students | 6 | 9 | 16 | 13 | 4 | 2 |
Solution
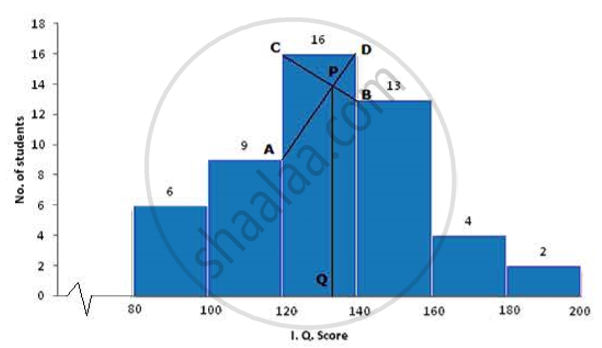
(a) Take 1cm = 1 unit and plot I. Q. Score on x-axis and no. of students on y axis.
(b) Draw a bar graph for the given data.
(c) From the histogram it is clear that class 120-140 has highest frequency i.e. 16
(d) Join the ends of the corresponding frequencies which meet at P and drop a perpendicular on the x-axis from P to Q. Q is the mode.
Therefore, Mode = 134
APPEARS IN
RELATED QUESTIONS
Using a graph paper draw a histogram of the given distribution showing the number of runs scored by 50 batsmen. Estimate the mode of the data:
| Runs scored |
3000- 4000 |
4000- 5000 |
5000- 6000 |
6000- 7000 |
7000- 8000 |
8000- 9000 |
9000- 10000 |
| No. of batsmen |
4 | 18 | 9 | 6 | 7 | 2 | 4 |
Find the mean of the following distribution by step deviation method:
| Class Interval | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Frequency | 10 | 6 | 8 | 12 | 5 | 9 |
Marks obtained (in mathematics) by 9 students are given below:
60, 67, 52, 76, 50, 51, 74, 45 and 56
- Find the arithmetic mean.
- If marks of each student be increased by 4; what will be the new value of arithmetic mean?
The following table shows the frequency distribution of heights of 51 boys:
| Height (cm) | 120 | 121 | 122 | 123 | 124 |
| Frequency | 5 | 8 | 18 | 10 | 9 |
Find the mode of heights.
A boy scored following marks in various class tests during a term; each test being marked out of 20.
15, 17, 16, 7, 10, 12, 14, 16, 19, 12 and 16
What are his total marks?
The heights of 9 persons are 142 cm, 158 cm, 152 cm, 143 cm, 139 cm, 144 cm, 146 cm, 148 cm and 151 cm. Find the mean height.
The mean of the following frequency distribution is 25.8 and the sum of all the frequencies is 50. Find x and y.
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| Frequency | 7 | x | 15 | y | 10 |
Find the median of the following:
3x, x+5, x+7, x+9, x+11, x+13
Find the mean of all factors of 10.
Find the median of the given values : 47, 53, 62, 71, 83, 21, 43, 47, 41
