Advertisements
Advertisements
Question
E°cell for the given redox reaction is 2.71V
\[\ce{Mg_{(s)} +Cu^{2+}_{(0.01 M)}->Mg^{2+}_{(0.001M)}+Cu_{(s)}}\]
Calculate Ecell for the reaction. Write the direction of flow of current when an external opposite potential applied is
(i) less than 2.71 V and
(ii) greater than 2.71 V
Solution
\[\ce{Mg_{(s)} +Cu^{2+}_{(aq)}->Mg^{2+}_{(aq)}+Cu_{(s)}}\]
Q=`(["Mg"^(2+)]["Cu"])/(["Mg"]["Cu"^2] `
`=((0.001)(1))/((1)(0.01))=0.1`
Using the Nernst equation,
Ecell = E°cell `-0.0591/"n" "log Q"`
Ecell`=2.71-0.0591/2 "log Q"`
Ecell=2.74V
(i) Since the voltage applied externally is less than cell E then the direction of flow of current is from cathode to anode
(ii) When the external voltage applied exceeds cell E, the direction of flow of current is from anode to cathode. If the voltage is applied is greater than 2.74V, the direction of current is from anode to cathode.
APPEARS IN
RELATED QUESTIONS
A jet plane is travelling towards west at a speed of 1800 km/h. What is the voltage difference developed between the ends of the wing having a span of 25 m, if the Earth’s magnetic field at the location has a magnitude of 5 × 10−4 T and the dip angle is 30°.
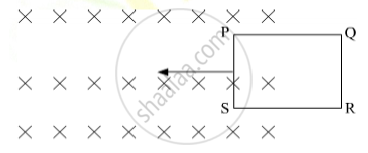
The closed loop (PQRS) of wire is moved into a uniform magnetic field at right angles to the plane of the paper as shown in the figure, Predict the direction of the induced current in the loop.
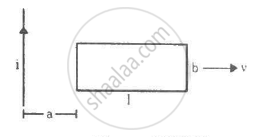
A rectangular metallic loop of length l and width b is placed coplanarly with a long wire carrying a current i (figure). The loop is moved perpendicular to the wire with a speed vin the plane containing the wire and the loop. Calculate the emf induced in the loop when the rear end of the loop is at a distance a from the wire. solve by using Faraday's law for the flux through the loop and also by replacing different segments with equivalent batteries.
A .0.5m long solenoid of 10 turns/cm has area of cross-section 1cm2 . Calculate the voltage induced across its ends if the current in the solenoid is changed from 1A to 2A in 0.1s.
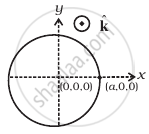
A magnetic field in a certain region is given by `B = B_o cos (ωt)hatk` and a coil of radius a with resistance R is placed in the x-y plane with its centre at the origin in the magnetic field (Figure) . Find the magnitude and the direction of the current at (a, 0, 0) at t = π/2ω, t = π/ω and t = 3π/2ω.
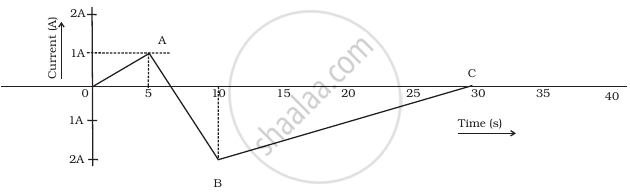
A (current vs time) graph of the current passing through a solenoid is shown in figure. For which time is the back electromotive force (u) a maximum. If the back emf at t = 3s is e, find the back emf at t = 7s, 15s and 40s. OA, AB and BC are straight line segments.
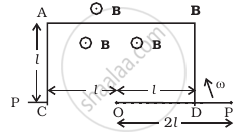
ODBAC is a fixed rectangular conductor of negilible resistance (CO is not connnected) and OP is a conductor which rotates clockwise with an angular velocity ω (Figure). The entire system is in a uniform magnetic field B whose direction is along the normal to the surface of the rectangular conductor ABDC. The conductor OP is in electric contact with ABDC. The rotating conductor has a resistance of λ per unit length. Find the current in the rotating conductor, as it rotates by 180°.
A coil of effective area 4 m2 is placed at right angles to the magnetic induction B. The e.m.f. of 0.32 V is induced in the coil. When the field is reduced to 20% of its initial value in 0.5 sec. Find B (in wb/m2).
A square-shaped coil of side 10 cm, having 100 turns is placed perpendicular to a magnetic field which is increasing at 1 T/s. The induced emf in the coil is ______.
