Advertisements
Advertisements
Question
ODBAC is a fixed rectangular conductor of negilible resistance (CO is not connnected) and OP is a conductor which rotates clockwise with an angular velocity ω (Figure). The entire system is in a uniform magnetic field B whose direction is along the normal to the surface of the rectangular conductor ABDC. The conductor OP is in electric contact with ABDC. The rotating conductor has a resistance of λ per unit length. Find the current in the rotating conductor, as it rotates by 180°.
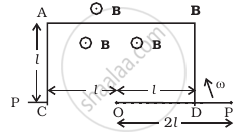
Solution
When the conductor OP is rotated, then the rate of change of area and hence the rate of change of flux can be considered uniform from `0 < θ < pi/4; pi/4 < θ < (3pi)/4` and `(3pi)/4 < θ < pi/2`.
(i) Let us first assume the position of rotating conductor at time interval
t = 0 to `t = pi/(4ω)` (or T/8)
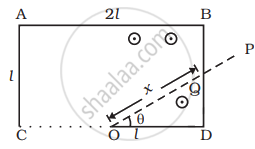
The rod OP will make contact with the side BD. Let the length OQ of the contact after some time interval t such that `0 < t < pi/(4ω)` or `ω < t < T/8` be x.
The flux through the area ODQ is `phi_m = BA = B(1/2 xx QD xx OD) = B(1/2 xx l tan θ x l)`
⇒ `phi_m = 1/2 Bl^2 tan θ`, where θ = ωt
By applying Faraday's law of EMI,
Thus, the magnitude of the emf induced is `|ε| = |(dphi)/(dt)| = 1/2 Bl^2 ω sec^2 ωt`
The current induced in the circuit will be `I = ε/R` where, R is the resistance of the rod in contact.
Where, `R oo λ`
R = `λx = (λl)/(cos ωt)`
∴ `I = 1/2 (Bl^2ω)/(λl) sec^2 ωt cos ωt = (Blω)/(2λ cos ωt)`
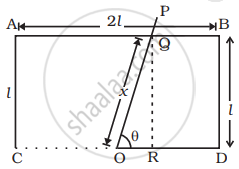
(ii) Now let the rod OP will make contact with the side AB. And the length of OQ of the contact after some time interval t such that `pi/(4ω) < t < (3pi)/(4ω)` or `T//8 < t < (3T)/8` be x.
The flux through the area OQBD is `phi_m = (l^2 + 1/2 l^2/(2 tan theta))B`
Where, θ = ωt
Thus, the magnitude of emf induced in the loop is
`|ε| = |(dphi)/(dt)| = (Bl^2 ω sec^2 ωt)/(2 tan^2 ωt)`
The current induced in the circuit is `I = ε/R = ε/(λx) = (ε sin ωt)/(λl) = 1/2 (Blω)/(λ sin ωt)`
(iii) When the flux through OQABD = `phi` = B.A
`phi = B.(2l^2 + 1/2 ly)`
`phi = B.(2l^2 + (l^2 tan ωt)/2)` ......`[(tan (180 - theta) = y/l),((y = l(- tan theta)),(y = - l tan theta))]`
`(dphi)/(dt) = d/(dt) [2l^2 + l^2/2 (tan ωt)]B`
`- ε = 0 + (Bl^2)/2 + d/(dt) tan ωt`
`- ε = + (Bl^2ω)/2 sec^2 ωt = - (Bl^2ω)/(2 cos^2 ωt)`
`I = ε/R = ε/(λx)`
`I = (- Bl^2ω)/(2 cos^2 ωt) (cos ωt)/(λ(-1))` ......`[because l/x = cos (180 - θ) 1/x = - cos θ ⇒ x = (-1)/(cos ωt)]`
| `I = (Blω)/(2λ cos ωt)` |
APPEARS IN
RELATED QUESTIONS
A circular coil of radius 8.0 cm and 20 turns is rotated about its vertical diameter with an angular speed of 50 rad s−1 in a uniform horizontal magnetic field of magnitude 3.0 × 10−2 T. Obtain the maximum and average emf induced in the coil. If the coil forms a closed loop of resistance 10 Ω, calculate the maximum value of current in the coil. Calculate the average power loss due to Joule heating. Where does this power come from?
A jet plane is travelling towards west at a speed of 1800 km/h. What is the voltage difference developed between the ends of the wing having a span of 25 m, if the Earth’s magnetic field at the location has a magnitude of 5 × 10−4 T and the dip angle is 30°.
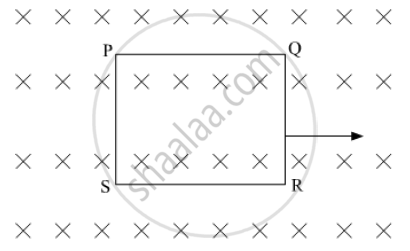
The closed loop (PQRS) of wire is moved into a uniform magnetic field at right angles to the plane of the paper as shown in the figure. Predict the direction of the induced current in the loop.
E°cell for the given redox reaction is 2.71V
\[\ce{Mg_{(s)} +Cu^{2+}_{(0.01 M)}->Mg^{2+}_{(0.001M)}+Cu_{(s)}}\]
Calculate Ecell for the reaction. Write the direction of flow of current when an external opposite potential applied is
(i) less than 2.71 V and
(ii) greater than 2.71 V
A 0⋅5 m long solenoid of 10 turns/cm has the area of cross-section 1 cm2. Calculate the voltage induced across its ends if the current in the solenoid is changed from 1 A to A in 0⋅1 s.
According to Faraday’s law of electromagnetic induction ______.
The average e.m.f induced in a coil in which current change from 0.2 ampere to 0.4 ampere in· 0.1 sec is 1 volt, the self-inductance of the coil is
A magnetic field B is confined to a region r ≤ a and points out of the paper (the z-axis), r = 0 being the centre of the circular region. A charged ring (charge = Q) of radius b, b > a and mass m lies in the x-y plane with its centre at the origin. The ring is free to rotate and is at rest. The magnetic field is brought to zero in time ∆t. Find the angular velocity ω of the ring after the field vanishes.
A coil of effective area 4 m2 is placed at right angles to the magnetic induction B. The e.m.f. of 0.32 V is induced in the coil. When the field is reduced to 20% of its initial value in 0.5 sec. Find B (in wb/m2).
The self induced emf of a coil is 25 volts. When the current in it is changed at uniform rate from 10 A to 25 A in 1 s, the change in the energy of the inductance is ______.
