Advertisements
Advertisements
प्रश्न
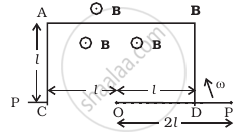
ODBAC is a fixed rectangular conductor of negilible resistance (CO is not connnected) and OP is a conductor which rotates clockwise with an angular velocity ω (Figure). The entire system is in a uniform magnetic field B whose direction is along the normal to the surface of the rectangular conductor ABDC. The conductor OP is in electric contact with ABDC. The rotating conductor has a resistance of λ per unit length. Find the current in the rotating conductor, as it rotates by 180°.
उत्तर
When the conductor OP is rotated, then the rate of change of area and hence the rate of change of flux can be considered uniform from `0 < θ < pi/4; pi/4 < θ < (3pi)/4` and `(3pi)/4 < θ < pi/2`.
(i) Let us first assume the position of rotating conductor at time interval
t = 0 to `t = pi/(4ω)` (or T/8)
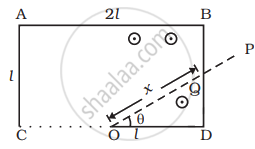
The rod OP will make contact with the side BD. Let the length OQ of the contact after some time interval t such that `0 < t < pi/(4ω)` or `ω < t < T/8` be x.
The flux through the area ODQ is `phi_m = BA = B(1/2 xx QD xx OD) = B(1/2 xx l tan θ x l)`
⇒ `phi_m = 1/2 Bl^2 tan θ`, where θ = ωt
By applying Faraday's law of EMI,
Thus, the magnitude of the emf induced is `|ε| = |(dphi)/(dt)| = 1/2 Bl^2 ω sec^2 ωt`
The current induced in the circuit will be `I = ε/R` where, R is the resistance of the rod in contact.
Where, `R oo λ`
R = `λx = (λl)/(cos ωt)`
∴ `I = 1/2 (Bl^2ω)/(λl) sec^2 ωt cos ωt = (Blω)/(2λ cos ωt)`
(ii) Now let the rod OP will make contact with the side AB. And the length of OQ of the contact after some time interval t such that `pi/(4ω) < t < (3pi)/(4ω)` or `T//8 < t < (3T)/8` be x.
The flux through the area OQBD is `phi_m = (l^2 + 1/2 l^2/(2 tan theta))B`
Where, θ = ωt
Thus, the magnitude of emf induced in the loop is
`|ε| = |(dphi)/(dt)| = (Bl^2 ω sec^2 ωt)/(2 tan^2 ωt)`
The current induced in the circuit is `I = ε/R = ε/(λx) = (ε sin ωt)/(λl) = 1/2 (Blω)/(λ sin ωt)`
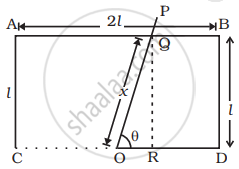
(iii) When the flux through OQABD = `phi` = B.A
`phi = B.(2l^2 + 1/2 ly)`
`phi = B.(2l^2 + (l^2 tan ωt)/2)` ......`[(tan (180 - theta) = y/l),((y = l(- tan theta)),(y = - l tan theta))]`
`(dphi)/(dt) = d/(dt) [2l^2 + l^2/2 (tan ωt)]B`
`- ε = 0 + (Bl^2)/2 + d/(dt) tan ωt`
`- ε = + (Bl^2ω)/2 sec^2 ωt = - (Bl^2ω)/(2 cos^2 ωt)`
`I = ε/R = ε/(λx)`
`I = (- Bl^2ω)/(2 cos^2 ωt) (cos ωt)/(λ(-1))` ......`[because l/x = cos (180 - θ) 1/x = - cos θ ⇒ x = (-1)/(cos ωt)]`
| `I = (Blω)/(2λ cos ωt)` |
APPEARS IN
संबंधित प्रश्न
A circular coil of radius 8.0 cm and 20 turns is rotated about its vertical diameter with an angular speed of 50 rad s−1 in a uniform horizontal magnetic field of magnitude 3.0 × 10−2 T. Obtain the maximum and average emf induced in the coil. If the coil forms a closed loop of resistance 10 Ω, calculate the maximum value of current in the coil. Calculate the average power loss due to Joule heating. Where does this power come from?
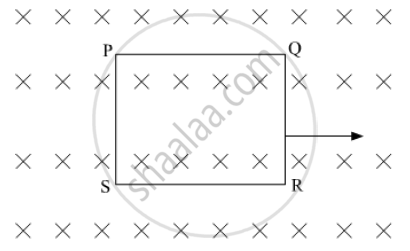
The closed loop (PQRS) of wire is moved into a uniform magnetic field at right angles to the plane of the paper as shown in the figure. Predict the direction of the induced current in the loop.
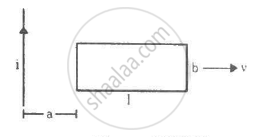
A rectangular metallic loop of length l and width b is placed coplanarly with a long wire carrying a current i (figure). The loop is moved perpendicular to the wire with a speed vin the plane containing the wire and the loop. Calculate the emf induced in the loop when the rear end of the loop is at a distance a from the wire. solve by using Faraday's law for the flux through the loop and also by replacing different segments with equivalent batteries.
A .0.5m long solenoid of 10 turns/cm has area of cross-section 1cm2 . Calculate the voltage induced across its ends if the current in the solenoid is changed from 1A to 2A in 0.1s.
E°cell for the given redox reaction is 2.71V
\[\ce{Mg_{(s)} +Cu^{2+}_{(0.01 M)}->Mg^{2+}_{(0.001M)}+Cu_{(s)}}\]
Calculate Ecell for the reaction. Write the direction of flow of current when an external opposite potential applied is
(i) less than 2.71 V and
(ii) greater than 2.71 V
A 0⋅5 m long solenoid of 10 turns/cm has the area of cross-section 1 cm2. Calculate the voltage induced across its ends if the current in the solenoid is changed from 1 A to A in 0⋅1 s.
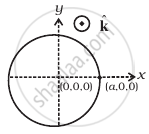
A magnetic field in a certain region is given by `B = B_o cos (ωt)hatk` and a coil of radius a with resistance R is placed in the x-y plane with its centre at the origin in the magnetic field (Figure) . Find the magnitude and the direction of the current at (a, 0, 0) at t = π/2ω, t = π/ω and t = 3π/2ω.
A magnetic field B is confined to a region r ≤ a and points out of the paper (the z-axis), r = 0 being the centre of the circular region. A charged ring (charge = Q) of radius b, b > a and mass m lies in the x-y plane with its centre at the origin. The ring is free to rotate and is at rest. The magnetic field is brought to zero in time ∆t. Find the angular velocity ω of the ring after the field vanishes.
A coil of effective area 4 m2 is placed at right angles to the magnetic induction B. The e.m.f. of 0.32 V is induced in the coil. When the field is reduced to 20% of its initial value in 0.5 sec. Find B (in wb/m2).
