Advertisements
Advertisements
प्रश्न
A magnetic field in a certain region is given by `B = B_o cos (ωt)hatk` and a coil of radius a with resistance R is placed in the x-y plane with its centre at the origin in the magnetic field (Figure) . Find the magnitude and the direction of the current at (a, 0, 0) at t = π/2ω, t = π/ω and t = 3π/2ω.
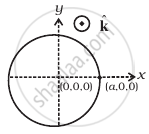
उत्तर
- First law: Whenever the number of magnetic lines of force (magnetic flux) passing through a circuit changes, an emf is produced in the circuit called induced emf. The induced emf persists only as long as there is a change or cutting of flux.
- Second law: The induced emf is given by the rate of charge of magnetic flux linked with the circuit, i.e, `e = - (dphi)/(dt)`. For N turns `e = - (N dphi)/(dt)`; NEgative sign indicates that induced emf (e) opposes the change of flux.
First we need to find out the flux passing through the ring at any instant and that is given by
`phi_m = vecB * vecA = BA cos theta`
And as we know both `vecA` (area vector) and `vecB` (magnetic field vector) are directed along z-axis. So, angle between them is 0.
So, cos θ = 1 .....(∵ θ = 0)
⇒ `phi_m = BA`
Area of coil of radius a = πa2
ε = `B_0(pia^2) cos ωt`
By Faraday's law of electromagnetic induction,
Magnitude of induced emf is given by ε = `B_0(pia^2) ω sin ωt`
This causes flow of indeed current, which is given by `I = (B_0(pia^2) ω sin ωt)/R`
Now, the value of current at different instants,
(i) `t = pi/(2ω)`
`I = (B_0(pia^2)ω)/R` along `hatj`
Because sin ωt = `sin(ω pi/(2ω)) = sin pi/2` = 1
(ii) `t = pi/ω, I = (B(pia^2)ω)/R` = 0
Because, sin ωt = `sin(ω pi/ω) = sin pi` = 0
(iii) `t = 3/2 pi/ω`
`I = (B(pia^2)ω)/R` along `-hatj`
sin ωt = `sin(ω * (3pi)/(2ω)) = sin (3pi)/2` = – 1
APPEARS IN
संबंधित प्रश्न
A jet plane is travelling towards west at a speed of 1800 km/h. What is the voltage difference developed between the ends of the wing having a span of 25 m, if the Earth’s magnetic field at the location has a magnitude of 5 × 10−4 T and the dip angle is 30°.
State Faraday's first law of electrolysis.
A 0⋅5 m long solenoid of 10 turns/cm has the area of cross-section 1 cm2. Calculate the voltage induced across its ends if the current in the solenoid is changed from 1 A to A in 0⋅1 s.
According to Faraday’s law of electromagnetic induction ______.
The average e.m.f induced in a coil in which current change from 0.2 ampere to 0.4 ampere in· 0.1 sec is 1 volt, the self-inductance of the coil is
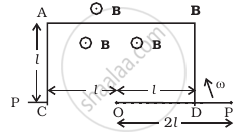
ODBAC is a fixed rectangular conductor of negilible resistance (CO is not connnected) and OP is a conductor which rotates clockwise with an angular velocity ω (Figure). The entire system is in a uniform magnetic field B whose direction is along the normal to the surface of the rectangular conductor ABDC. The conductor OP is in electric contact with ABDC. The rotating conductor has a resistance of λ per unit length. Find the current in the rotating conductor, as it rotates by 180°.
A magnetic field B is confined to a region r ≤ a and points out of the paper (the z-axis), r = 0 being the centre of the circular region. A charged ring (charge = Q) of radius b, b > a and mass m lies in the x-y plane with its centre at the origin. The ring is free to rotate and is at rest. The magnetic field is brought to zero in time ∆t. Find the angular velocity ω of the ring after the field vanishes.
A coil of effective area 4 m2 is placed at right angles to the magnetic induction B. The e.m.f. of 0.32 V is induced in the coil. When the field is reduced to 20% of its initial value in 0.5 sec. Find B (in wb/m2).
The self induced emf of a coil is 25 volts. When the current in it is changed at uniform rate from 10 A to 25 A in 1 s, the change in the energy of the inductance is ______.
Two coils C1 and C2 are placed close to each other. The magnetic flux Φ2 linked with coil C2 varies with the current I1 flowing in coil C1 as shown in the figure. Find
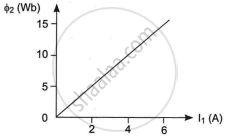
- The mutual inductance of the arrangement, and
- The rate of change of current `((dI_1)/(dt))` will induce an emf of 100V in coil C2.
