Advertisements
Advertisements
Question
एक व्यक्ति दौड़पथ पर दौड़ते हुऐ अंकित करता है कि उससे दो झंडा चौकियों की दूरियों का योग सदैव 10 मीटर रहता है। और झंडा चौकियों के बीच की दूरी 8 मीटर है। व्यक्ति द्वारा बनाए पथ का समीकरण ज्ञात कीजिए।
Solution
मान लीजिए कि F1 और F2 दो बिंदु हैं जहाँ झंडा चौकियां जमीन पर लगे हुए हैं।
मूल बिंदु O, F1F2 का मध्य-बिंदु है।
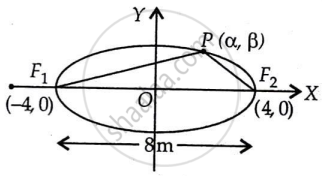
∴ OF1 - OF2 = `1/2 F_1F_2 = 1/2 xx 8 = 4"मीटर" `
F1 के निर्देशांक (-4, 0) हैं और F2 के निर्देशांक (4, 0) हैं
मान लीजिए P (α, β) पथ पर कोई बिंदु है।
∴ PF1 + PF2 = 10
∴ `sqrt((α + 4)^2 + (β - 0)^2)` + `sqrt((α - 4)^2 + (β - 0)^2) = 10`
= `sqrt(α^2 + 16 + 8α + β^2)` = `10 - sqrt(α^2 + 16 - 8α + β^2)`
दोनों पक्षों का वर्ग करने पर, हमें प्राप्त होता है
α2 + β2 + 8α + 16 = 100 + α2 + β2 - Bα + 16 `-20 sqrt(α^2 + β^2 - 8α + 16)`
= 16α - 100 = `-20 sqrt(α^2 + β^2 - 8α + 16)`
पुनः, दोनों पक्षों का वर्ग करने पर, हमें प्राप्त होता है
= (16α - 100)2 = (`-20 sqrt((α^2 + β^2 - 8α + 16)^2)`
= 256α2 + 10000 - 3200α = 400(α2 + β2 - 8α+ 16)
= 256α2 + 10000 - 3200α = 400α2 + 400β2 - 32008α+ 6400)
= 144α2 + 400β2 = 3600
= `(144α^2)/(3600) + (400β^2)/(3600) = 1`
इस प्रकार, बिंदु P के बिंदुपथ का आवश्यक समीकरण `x^2/25 + y^2/9 = 1` है।
APPEARS IN
RELATED QUESTIONS
निम्नलिखित प्रश्न में, दिए प्रतिबंध को संतुष्ट करते हुए दीर्घवृत्त का समीकरण ज्ञात कीजिए:
शीर्षों (±5, 0), नाभियाँ (±4, 0)
निम्नलिखित प्रश्न में, दिए प्रतिबंधों को संतुष्ट करते हुए दीर्घवृत्त का समीकरण ज्ञात कीजिए:
शीर्षों (0, ±13), नाभियाँ (0, ±5)
निम्नलिखित प्रश्न में, दिए प्रतिबंधों को संतुष्ट करते हुए दीर्घवृत्त का समीकरण ज्ञात कीजिए:
शीर्ष (±6, 0), नाभियाँ (±4, 0)
निम्नलिखित प्रश्न में, दिए प्रतिबंधों को संतुष्ट करते हुए दीर्घवृत्त का समीकरण ज्ञात कीजिए:
दीर्घ अक्ष के अंत्य बिंदु (±3, 0), लघु अक्ष के अंत्य बिंदु (0, ±2).
निम्नलिखित प्रश्न में, दिए प्रतिबंधों को संतुष्ट करते हुए दीर्घवृत्त का समीकरण ज्ञात कीजिए:
दीर्घ अक्ष के अंत्य बिंदु (0, ±`sqrt5`), लघु अक्ष के अंत्य बिंदु (±1, 0)
निम्नलिखित प्रश्न में, दिए प्रतिबंधों को संतुष्ट करते हुए दीर्घवृत्त का समीकरण ज्ञात कीजिए:
दीर्घ अक्ष की लंबाई 26, नाभियाँ (±5, 0)
एक मेहराव अर्ध-दीर्घवृत्ताकार रूप का है। यह 8 मीटर चौड़ा है और केंद्र से 2 मीटर ऊँचा है। एक सिरे से 1.5 मीटर दूर बिंदु पर मेहराव की ऊँचाई ज्ञात कीजिए।
एक 12 सेमी लंबी छड़ इस प्रकार चलती है कि इसके सिरे निर्देशांक्षों को स्पर्श करते हैं। छड़ के बिंदु P का बिंदुपथ ज्ञात कीजिए जो x-अक्ष के संपर्क वाले सिरे से 3 सेमी दूर है।
