Advertisements
Advertisements
Question
Evaluate the following
tan2 30° + tan2 60° + tan2 45°
Solution
tan2 30° + tan2 60° + tan2 45° ....(i)
By trigonometric ratios we have
`tan 30^@ = 1/sqrt3 tan 60^@ = sqrt3 tan 45^@ = 1`
By substituting above values in (i), we get
`[1/sqrt3]^2 + [sqrt3]^2 + [1]^2`
`=> 1/3 + 3 + 1 => 1/3 + 4`
`=> (1 + 12)/3 = 13/3`
APPEARS IN
RELATED QUESTIONS
If `cot theta = 1/sqrt3` show that `(1 - cos^2 theta)/(2 - sin^2 theta) = 3/5`
Evaluate the Following
`cot^2 30^@ - 2 cos^2 60^circ- 3/4 sec^2 45^@ - 4 sec^2 30^@`
If cos (81 + θ)° = sin`("k"/3 - theta)^circ` where θ is an acute angle, then the value of k is ______.
3 sin² 20° – 2 tan² 45° + 3 sin² 70° is equal to ______.
If cos A = `4/5`, then the value of tan A is ______.
Prove the following:
If tan A = `3/4`, then sinA cosA = `12/25`
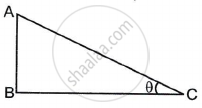
In ΔABC, ∠ABC = 90° and ∠ACB = θ. Then write the ratios of sin θ and tan θ from the figure.
Let tan9° = `(1 - sqrt((sqrt(5)k)/m))k` where k = `sqrt(5) + 1` then m is equal to ______.
The maximum value of the expression 5cosα + 12sinα – 8 is equal to ______.
If cosec θ = `("p" + "q")/("p" - "q")` (p ≠ q ≠ 0), then `|cot(π/4 + θ/2)|` is equal to ______.
