Advertisements
Advertisements
Question
Evaluate Rydberg constant by putting the values of the fundamental constants in its expression.
Solution
Expression of Rydberg constant (R) is given by
`R = (me^4)/(8h^2c ∈_0^2)`
Mass of electron, me = `9.31 xx 10^21 xx kg `
Charge, e = 1.6 × 10−19 C
]Planck's constant, h = 6.63 × 10−34 J-s,
Speed of light, c = 3 × 108 m/s,
Permittivity of vacuum, ∈0 = 8.85 × 10−12 C2N1m
On substituting the values in the expression, we get
`R = ((9.31xx10^-31)xx(1.6xx10^-19)^4)/(8 xx(6.63xx10^-14)^2 xx (3xx10^8)xx(8.85xx10^-12)^2`
`rArr R = 1.097 xx 10^7 m^-1`
APPEARS IN
RELATED QUESTIONS
(i) State Bohr's quantization condition for defining stationary orbits. How does the de Broglie hypothesis explain the stationary orbits?
(ii) Find the relation between three wavelengths λ1, λ2 and λ3 from the energy-level diagram shown below.
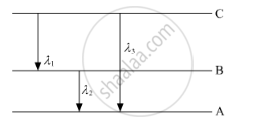
What is the maximum number of emission lines when the excited electron of an H atom in n = 6 drops to the ground state?
Explain, giving reasons, which of the following sets of quantum numbers are not possible.
(a) n = 0, l = 0, ml = 0, ms = + ½
(b) n = 1, l = 0, ml = 0, ms = – ½
(c) n = 1, l = 1, ml = 0, ms = + ½
(d) n = 2, l = 1, ml = 0, ms = – ½
(e) n = 3, l = 3, ml = –3, ms = + ½
(f) n = 3, l = 1, ml = 0, ms = + ½
How many electrons in an atom may have the following quantum numbers?
n = 4, `m_s = -1/2`
Calculate the energy required for the process
\[\ce{He^+_{(g)} -> He^{2+}_{(g)} + e^-}\]
The ionization energy for the H atom in the ground state is 2.18 ×10–18 J atom–1
(a) Using the Bohr’s model calculate the speed of the electron in a hydrogen atom in the n = 1, 2, and 3 levels.
(b) Calculate the orbital period in each of these levels.
In Bohr’s model of the hydrogen atom, the radius of the first orbit of an electron is r0 . Then, the radius of the third orbit is:
a) `r_0/9`
b) `r_0`
c) `3r_0`
d) `9r_0`
Using Bohr’s postulates for hydrogen atom, show that the total energy (E) of the electron in the stationary states tan be expressed as the sum of kinetic energy (K) and potential energy (U), where K = −2U. Hence deduce the expression for the total energy in the nth energy level of hydrogen atom.
Which of the following parameters are the same for all hydrogen-like atoms and ions in their ground states?
Find the wavelength of the radiation emitted by hydrogen in the transitions (a) n = 3 to n= 2, (b) n = 5 to n = 4 and (c) n = 10 to n = 9.
Write postulates of Bohr’s Theory of hydrogen atom.
Mention demerits of Bohr’s Atomic model.
The spectral line obtained when an electron jumps from n = 5 to n = 2 level in hydrogen atom belongs to the ____________ series.
According to Bohr’s theory, the angular momentum of an electron in 5th orbit is ______.
For an electron in the second orbit of hydrogen, what is the moment of momentum as per the Bohr's model?
Hydrogen atom has only one electron, so mutual repulsion between electrons is absent. However, in multielectron atoms mutual repulsion between the electrons is significant. How does this affect the energy of an electron in the orbitals of the same principal quantum number in multielectron atoms?
Taking the Bohr radius as a0 = 53 pm, the radius of Li++ ion in its ground state, on the basis of Bohr’s model, will be about ______.
A 100 eV electron collides with a stationary helium ion (He+) in its ground state and exits to a higher level. After the collision, He+ ions emit two photons in succession with wavelengths 1085 Å and 304 Å. The energy of the electron after the collision will be ______ eV.
Given h = 6.63 × 10-34 Js.
Specify the transition of an electron in the wavelength of the line in the Bohr model of the hydrogen atom which gives rise to the spectral line of the highest wavelength ______.
On the basis of Bohr's theory, derive an expression for the radius of the nth orbit of an electron of hydrogen atom.
