Advertisements
Advertisements
Question
Express the truth of each of the following statements using Venn diagrams:
(a) No circles are polygons
(b) Some quadratic equations have equal roots
Solution
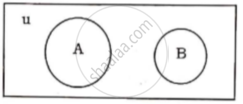
(a) Let u: The set of closed geometrical figures in the plane.
Let A: The set of all polygons and
B: The set of all circles
Hence the following is the Venn diagram.
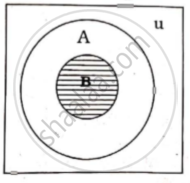
(b) Let u: The set of all equations.
Let A: The set of all quadratic equations and
B: The set of all quadratic, equations having equal roots.
Hence the following is the Venn d6agram.
APPEARS IN
RELATED QUESTIONS
Draw appropriate Venn diagram for the following:
A' ∩ B'
Draw appropriate Venn diagram for the following:
A' ∪ B'
If A and B are two set such that \[A \subset B\]then find:
\[A \cap B\]
If A and B are two sets such that \[A \subset B\] then find:
\[A \cup B\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[B \cup C\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find\[B \cup D\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[A \cup B \cup C\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[A \cup B \cup D\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[B \cup C \cup D\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[A \cap \left( B \cup C \right)\]
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\]and D = {x : x is a prime natural number}. Find: \[A \cap B\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}. Find: \[A - C\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}.
Find: \[B - C\]
Take the set of natural numbers from 1 to 20 as universal set and show set Y using Venn diagram.
Y = {y | y ∈ N, y is prime number from 1 to 20}
Express the truth of each of the following statements using Venn diagram.
(1) All teachers are scholars and scholars are teachers.
(2) If a quadrilateral is a rhombus then it is a parallelogram..
From the given diagram find :
A ∪ B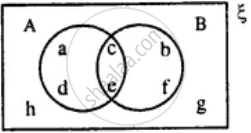
From the given diagram find :
B - A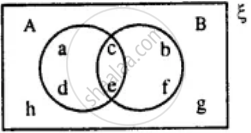
Use the given Venn-diagram to find :
A ∩ B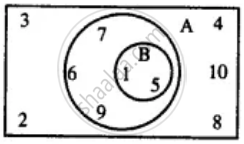
Use the given Venn-diagram to find :
A ∪ B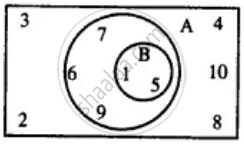
Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
A ∪ B
Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
B - A
Two sets A and B are such that A ∩ B = Φ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing :
A ∪ B
Two sets A and B are such that A ∩ B = Φ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing :
B - A
In the given diagram, shade the region which represents the set given underneath the diagrams: (A ∩ B)'
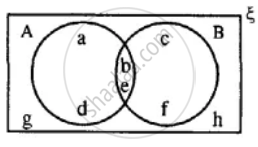
Using the given diagram, express the following sets in the terms of A and B. {a, d}
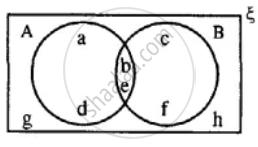
Using the given diagram, express the following sets in the terms of A and B. {g, h}
Represent the truth of the following statement by the Venn diagram.
No circles are polygons.
Represent the truth of the following statement by the Venn diagram.
If a quadrilateral is a rhombus, then it is a parallelogram.
Draw a Venn diagram for the truth of the following statement.
Some share brokers are chartered accountants.
Draw a Venn diagram for the truth of the following statement.
No wicket keeper is bowler, in a cricket team.
Express the truth of the following statement by the Venn diagram.
Some persons are not politician.
Express the truth of the following statement by the Venn diagram.
No child is an adult.
Draw the Venn diagrams to illustrate the following relationship among sets E, M and U, where E is the set of students studying English in a school, M is the set of students studying Mathematics in the same school, U is the set of all students in that school.
All the students who study Mathematics study English, but some students who study English do not study Mathematics.
Let U be the set of all boys and girls in a school, G be the set of all girls in the school, B be the set of all boys in the school, and S be the set of all students in the school who take swimming. Some, but not all, students in the school take swimming. Draw a Venn diagram showing one of the possible interrelationship among sets U, G, B and S.
Draw Venn diagram for the following:
No policeman is thief
