Advertisements
Advertisements
Question
Draw a Venn diagram for the truth of the following statement.
Some share brokers are chartered accountants.
Solution
Let U : The set of all human beings.
S : The set of all share brokers.
C : The set of all chartered accountants.
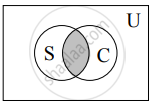
The above Venn diagram represents the truth of the given statement i.e., S ∩ C ≠ φ.
APPEARS IN
RELATED QUESTIONS
Express the truth of each of the following statements by Venn diagram:
(a) Some hardworking students are obedient.
(b) No circles are polygons.
(c) All teachers are scholars and scholars are teachers.
Draw appropriate Venn diagram for the following:
(A ∩ B)'
In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only.
Draw a Venn diagram for the truth of the following statement :
All rational number are real numbers.
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[B \cup C\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find\[B \cup D\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[A \cup B \cup C\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[\left( A \cup D \right) \cap \left( B \cup C \right)\]
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\] and D = {x : x is a prime natural number}. Find: \[B \cap C\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}. Find: \[A - C\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}.
Find: \[B - C\]
- show the sets U, P and P' by the Venn diagram.
- Verify (P')' = P
Represent the union of two sets by Venn diagram for the following.
A = {3, 4, 5, 7} B = {1, 4, 8}
Represent the union of two sets by Venn diagram for the following.
P = {a, b, c, e, f} Q = {l, m, n, e, b}
Represent the union of two sets by Venn diagram for the following.
Y = {y | y is an odd number between 90 and 100}
Express the truth of each of the following statements using Venn diagrams:
(a) No circles are polygons
(b) Some quadratic equations have equal roots
From the given diagram find :
A ∪ B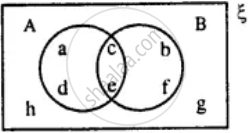
From the given diagram, find:
(i) A’
(ii) B’
(iii) A' ∪ B'
(iv) (A ∩ B)'
Is A' ∪ B' = (A ∩ B)' ?
Also, verify if A' ∪ B' = (A ∩ B)'.
Use the given Venn-diagram to find :
A ∩ B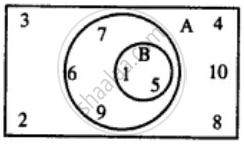
Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
A ∩ B
Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
A ∪ B
Draw a Venn-diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing :
A ∩ B
Two sets A and B are such that A ∩ B = Φ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing :
B ∩ A'
State the sets representing by the shaded portion of following venn-diagram :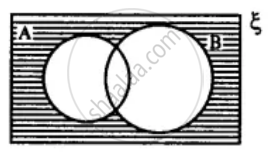
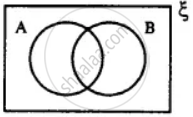
In the given diagram, shade the region which represents the set given underneath the diagrams: (B - A)'
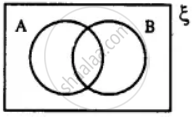
In the given diagram, shade the region which represents the set given underneath the diagrams: (A ∩ B)'
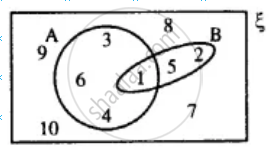
From the given diagram, find :
(i) (A ∪ B) - C
(ii) B - (A ∩ C)
(iii) (B ∩ C) ∪ A
Verify :
A - (B ∩ C) = (A - B) ∪ (A - C)

Using the given diagram, express the following sets in the terms of A and B. {a, d, c, f, g, h}
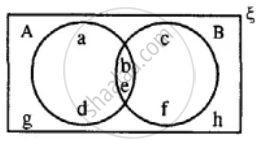
Using the given diagram, express the following sets in the terms of A and B. {a, d, g, h}
Represent the truth of the following statement by the Venn diagram.
All teachers are scholars and scholars are teachers.
Represent the truth of the following statement by the Venn diagram.
If a quadrilateral is a rhombus, then it is a parallelogram.
Represent the following statement by the Venn diagram.
If n is a prime number and n ≠ 2, then it is odd.
Express the truth of the following statement by the Venn diagram.
All men are mortal.
Draw the Venn diagrams to illustrate the following relationship among sets E, M and U, where E is the set of students studying English in a school, M is the set of students studying Mathematics in the same school, U is the set of all students in that school.
There is no student who studies both Mathematics and English.
Take the set of natural numbers from 1 to 20 as universal set and show set X using Venn diagram.
X = {x | x ∈ N, and 7 < x < 15}
