Advertisements
Advertisements
Question
Represent the following statement by the Venn diagram.
If n is a prime number and n ≠ 2, then it is odd.
Solution
Let, U : The set of all real numbers.
P : The set of all prime numbers n and n ≠ 2.
O : The set of all odd numbers.
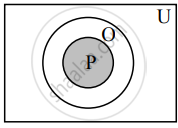
The above Venn diagram represents the truth of the given statement i.e., P ⊂ O.
APPEARS IN
RELATED QUESTIONS
Draw appropriate Venn diagram for the following:
A' ∪ B'
Draw Venn diagram for the truth of the following statements :
Some rectangles are squares.
If A and B are two set such that \[A \subset B\]then find:
\[A \cap B\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[B \cup C\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find\[B \cup D\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[B \cup C \cup D\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[\left( A \cup D \right) \cap \left( B \cup C \right)\]
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\]and D = {x : x is a prime natural number}. Find: \[A \cap B\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}. Find:
\[B - A\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}. Find: \[C - A\]
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {2, 4, 6, 8} and B = {2, 3, 5, 7}. Verify that \[\left( A \cup B \right)' = A' \cap B'\]
Take the set of natural numbers from 1 to 20 as universal set and show set Y using Venn diagram.
Y = {y | y ∈ N, y is prime number from 1 to 20}
- show the sets U, P and P' by the Venn diagram.
- Verify (P')' = P
Represent the union of two sets by Venn diagram for the following.
P = {a, b, c, e, f} Q = {l, m, n, e, b}
Represent the union of two sets by Venn diagram for the following.
Y = {y | y is an odd number between 90 and 100}
Express the truth of each of the following statements using Venn diagrams:
(a) No circles are polygons
(b) Some quadratic equations have equal roots
Express the truth of each of the following statements by Venn diagram :
(a) Some hardworking students are obedient.
(b) No circles are polygons.
(c) All teachers are scholars and scholars are teachers.
From the given diagram find :
A ∪ B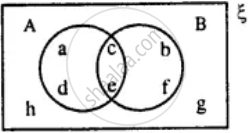
From the given diagram find :
A' ∩ B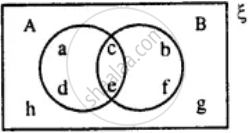
From the given diagram find :
B - A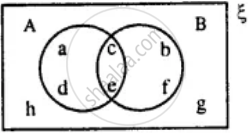
From the given diagram find :
(A ∪ B)'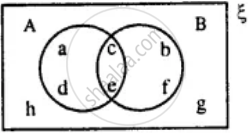
Use the given Venn-diagram to find :
A ∩ B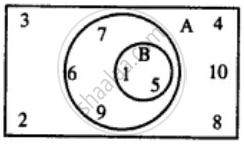
Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
A ∪ B
Draw a Venn-diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing :
A ∪ B
Draw a Venn-diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing :
(A ∪ B)'
State the sets representing by the shaded portion of following venn-diagram :
State the sets representing by the shaded portion of following venn-diagram :
In the given diagram, shade the region which represents the set given underneath the diagrams: (B - A)'
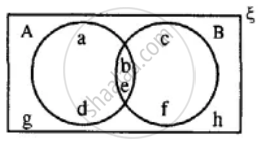
Using the given diagram, express the following sets in the terms of A and B. {a, d, c, f}
Represent the truth of the following statement by the Venn diagram.
Some hardworking students are obedient.
Represent the truth of the following statement by the Venn diagram.
If a quadrilateral is a rhombus, then it is a parallelogram.
Draw a Venn diagram for the truth of the following statement.
Some share brokers are chartered accountants.
Draw a Venn diagram for the truth of the following statement.
No wicket keeper is bowler, in a cricket team.
Express the truth of the following statement by the Venn diagram.
Some persons are not politician.
Draw Venn diagram for the following:
Some doctors are rich
Take the set of natural numbers from 1 to 20 as universal set and show set X using Venn diagram.
X = {x | x ∈ N, and 7 < x < 15}
