Advertisements
Advertisements
Question
Father's age is three times the sum of age of his two children. After 5 years his age will be twice the sum of ages of two children. Find the age of father.
Solution
Let the present age of father be x years and the present ages of his two children’s be y and zyears.
The present age of father is three times the sum of the ages of the two children’s. Thus, we have
`x=3(y+2)`
`⇒ y+z=x/5`
After 5 years, father’s age will be (x+5) years and the children’s age will be (y+5) and (z+5) years. Thus using the given information, we have
`x+5 =2 {(y+5)+(z+5)}`
`⇒ x+5 =2 (y+5+z+5)`
`⇒ x = 2(y+z)+20-5`
`⇒ x = 2 (y+z)+15`
So, we have two equations
`y+z =x/3`
`x=2(y+z)+15`
Here x, y and z are unknowns. We have to find the value of x.
Substituting the value of (y+z) from the first equation in the second equation, we have
By using cross-multiplication, we have
`x = (2x)/3+15`
`⇒ x=(2x)/3=15`
`⇒ x(1-2/3)=15`
`⇒ x/3=15`
`⇒ x= 15xx3`
`⇒ x =45`
Hence, the present age of father is 45 years.
APPEARS IN
RELATED QUESTIONS
Formulate the following problems as a pair of equations, and hence find their solutions:
Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current
A train covered a certain distance at a uniform speed. If the train would have been 10 km/h faster, it would have taken 2 hours less than the scheduled time. And if the train were slower by 10 km/h; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
Draw the graphs of the equations 5x − y = 5 and 3x − y = 3. Determine the coordinates of the vertices of the triangle formed by these lines and the y axis.
Solve the following pair of linear equations: px + qy = p − q, qx − py = p + q
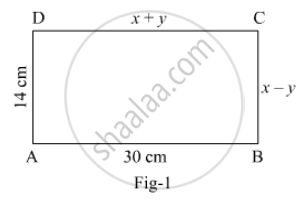
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
Find the values of following determinant.
`|(7/3,5/3), (3/2, 1/2)|`
The sum of digits of a two digit number is 13. If the number is subtracted from the one obtained by interchanging the digits, the result is 45. What is the number?
A two-digit number is 3 more than 4 times the sum of its digits. If 8 is added to the number, the digits are reversed. Find the number.
The numerator of a fraction is 4 less than the denominator. If the numerator is decreased by 2 and denominator is increased by 1, then the denominator is eight times the numerator. Find the fraction.
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
If 3 is added to the denominator and 2 is subtracted from the numerator, the fraction becomes `1/4`. Thus, we have
`(x-2)/(y+3)=1/4`
`⇒ 4(x-2)=y+3`
`⇒ 4x-8=y+3`
`⇒ 4x-y-11=0`
If 6 is added to the numerator and the denominator is multiplied by 3, the fraction becomes `2/3`. Thus, we have
`(x+6)/(3y)=2/3`
`⇒ 3(x+6)=6y`
`⇒ 3x +18 =6y`
`⇒ 3x-6y+18=0`
`⇒ 3(x-2y+6)=0`
`⇒ x-3y+6=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/((-1)xx6-(-2)xx(-11))=(-y)/(4xx6-1xx(-11))=1/(4xx(-2)-1xx(-1))`
`⇒ x/(-6-22)=-y/(24+11)=1/(-8+1)`
`⇒ x/-28=-y/35=1/-7`
`⇒ x= 28/7,y=35/7`
`⇒ x= 4,y=5`
Hence, the fraction is`4/5`
