Advertisements
Advertisements
Question
Fill in the blank :
Area of the region bounded by x2 = 16y, y = 1, y = 4 and the Y-axis, lying in the first quadrant is _______.
Solution
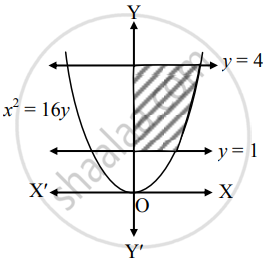
Required area = `int_1^4x*dy`
= `int_1^4 4sqrt(y)*dy`
= `4[y^(3/2)/(3/2)]_1^4`
= `(8)/(3)[(4)^(3/2) - (1)^(3/2)]`
= `(8)/(3)(8 - 1)`
= `(56)/(3)"sq.units"`.
APPEARS IN
RELATED QUESTIONS
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32.
The area between x = y2 and x = 4 is divided into two equal parts by the line x = a, find the value of a.
Find the area enclosed between the parabola y2 = 4ax and the line y = mx
Find the area of the smaller region bounded by the ellipse `x^2/a^2 + y^2/b^2 = 1` and the line `x/a + y/b = 1`
Find the equation of an ellipse whose latus rectum is 8 and eccentricity is `1/3`
Find the area of the region bounded by the following curves, the X-axis and the given lines: y = x4, x = 1, x = 5
Find the area of the region bounded by the parabola y2 = 4x and the line x = 3.
Choose the correct alternative :
Area of the region bounded by the curve x2 = y, the X-axis and the lines x = 1 and x = 3 is _______.
State whether the following is True or False :
The area bounded by the curve x = g (y), Y-axis and bounded between the lines y = c and y = d is given by `int_"c"^"d"x*dy = int_(y = "c")^(y = "d") "g"(y)*dy`
Solve the following :
Find the area of the region bounded by y = x2, the X-axis and x = 1, x = 4.
Solve the following:
Find the area of the region bounded by the curve x2 = 25y, y = 1, y = 4 and the Y-axis.
The area of the region x2 = 4y, y = 1 and y = 2 and the Y axis lying in the first quadrant is ______
The area of the region bounded by y2 = 25x, x = 1 and x = 2 the X axis is ______
Find area of the region bounded by the parabola x2 = 4y, the Y-axis lying in the first quadrant and the lines y = 3
If `int_0^(pi/2) log (cos x) "dx" = - pi/2 log 2,` then `int_0^(pi/2) log (cosec x)`dx = ?
Area bounded by the curve xy = 4, X-axis between x = 1, x = 5 is ______.
The equation of curve through the point (1, 0), if the slope of the tangent to t e curve at any point (x, y) is `(y - 1)/(x^2 + x)`, is
Find the area between the two curves (parabolas)
y2 = 7x and x2 = 7y.
If the area enclosed by y = f(x), X-axis, x = a, x = b and y = g(x), X-axis, x = a, x = b are equal, then f(x) = g(x).
