Advertisements
Advertisements
Question
Find the altitude of a trapezium whose area is 65 cm2 and whose bases are 13 cm and 26 cm.
Solution
Given:
Area of the trapezium=65 cm2
The lengths of the opposite parallel sides are 13 cm and 26 cm.
Area of trapezium\[=\frac{1}{2}\times(\text{ Sum of parallel bases })\times(\text{ Altitude })\]
On putting the values:
\[65 = \frac{1}{2} \times (13 + 26) \times (\text{ Altitude })\]
\[65 \times 2 = 39 \times\text{ Altitude }\]
\[\text{ Altitude }=\frac{130}{39}=\frac{10}{3}cm\]
APPEARS IN
RELATED QUESTIONS
Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.

Find the area, in square metres, of the trapezium whose bases and altitude is as under:
bases = 28 cm and 3 dm, altitude = 25 cm
Find the area of a trapezium whose parallel sides are of length 16 dm and 22 dm and whose height is 12 dm.
The area of a trapezium is 960 cm2. If the parallel sides are 34 cm and 46 cm, find the distance between them.
Top surface of a table is trapezium in shape. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.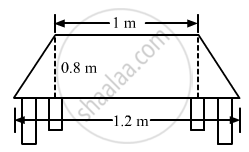
The area of a trapezium is 91 cm2 and its height is 7 cm. If one of the parallel sides is longer than the other by 8 cm, find the two parallel sides.
There is a pentagonal shaped park as shown in Fig. 20.50. Jyoti and Kavita divided it in two different ways.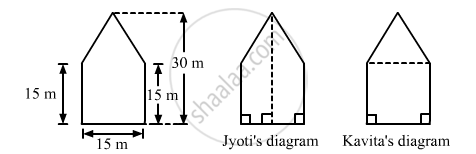
Find the area of this park using both ways. Can you suggest some another way of finding its areas?
Find the area of a trapezium whose parallel sides are 24 cm and 20 cm and the distance between them is 15 cm
When the non-parallel sides of a trapezium are equal then it is known as
A trapezium with 3 equal sides and one side double the equal side can be divided into ______ equilateral triangles of ______ area.
