Advertisements
Advertisements
Question
Find the height of a trapezium, the sum of the lengths of whose bases (parallel sides) is 60 cm and whose area is 600 cm2.
Solution
Given:
Sum of the parallel sides of a trapezium = 60 cm
\[ {\text{ Area of the trapezium }= 600 cm}^2 \]
\[\text{ Area of trapezium }=\frac{1}{2}\times(\text{ Sum of the parallel sides })\times(\text{ Height })\]
On putting the values:
\[600 = \frac{1}{2} \times 60 \times (\text{ Height })\]
\[600 = 30 \times (\text{ Height })\]
\[\text{ Height }=\frac{600}{30}= 20 cm\]
APPEARS IN
RELATED QUESTIONS
Find the area, in square metres, of the trapezium whose bases and altitude is as under:
bases = 28 cm and 3 dm, altitude = 25 cm
Find the area, in square metres, of the trapezium whose bases and altitude is as under:
bases = 8 m and 60 dm, altitude = 40 dm
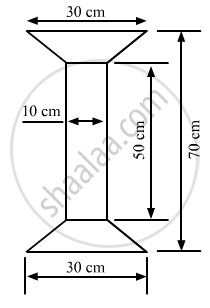
Find the area of Fig. as the sum of the areas of two trapezium and a rectangle.
Top surface of a table is trapezium in shape. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.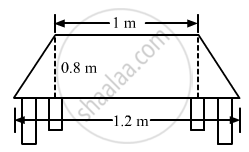
The area of a trapezium is 91 cm2 and its height is 7 cm. If one of the parallel sides is longer than the other by 8 cm, find the two parallel sides.
Find the area enclosed by each of the following figures [Fig. 20.49 (i)-(iii)] as the sum of the areas of a rectangle and a trapezium: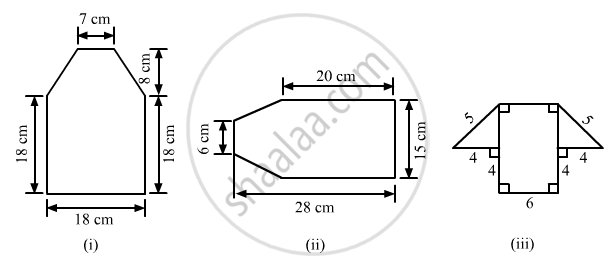
The two parallel sides and the distance between them are in the ratio 3: 4: 2. If the area of the trapezium is 175 cm2, find its height.
Find the missing values.
| Height 'h' | Parallel side 'a` | Parallel side 'b` | Area |
| 16 cm | 15 cm | 360 sq.cm |
The area of a trapezium is 1080 sq.cm. If the lengths of its parallel sides are 55.6 cm and 34.4 cm. Find the distance between them
A window is in the form of trapezium whose parallel sides are 105 cm and 50 cm respectively and the distance between the parallel sides is 60 cm. Find the cost of the glass used to cover the window at the rate of ₹ 15 per 100 sq.cm
