Advertisements
Advertisements
Question
A ray of light passes through an equilateral glass prism such that the angle of incidence is equal to the angle of emergence and each of these angles is equal to 3/4 of angle of prism. Find the angle of deviation.
Solution
The angle of deviation δ for a ray of light in a prism is given by
δ=i+e−A
where
i = Angle of incidence of ray
e = Its angle of emergence
A = Angle of prism
`∵e=i`
` ⇒δ=2i−A`
Given:` i=e=3/4A`
`∴δ=2×3/4A−A`
`⇒δ=1/2A`
As the prism is equailateral,⇒A=60°
`∴δ=12×60°`
`⇒δ=30`
APPEARS IN
RELATED QUESTIONS
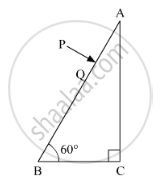
A ray PQ incident normally on the refracting face BA is refracted in the prism BAC made of material of refractive index 1.5. Complete the path of ray through the prism. From which face will the ray emerge? Justify your answer.
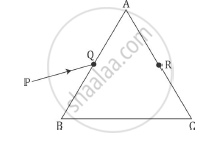
A ray PQ incident on the face AB of a prism ABC, as shown in the figure, emerges from the face AC such that AQ = AR.
Draw the ray diagram showing the passage of the ray through the prism. If the angle of the prism is 60° and refractive index of the material of prism is `sqrt3` , determine the values of angle of incidence and angle of deviation
If a glass prism is dipped in water, its dispersive power ___________ .
A prism can produce a minimum deviation δ in a light beam. If three such prisms are combined, the minimum deviation that can be produced in this beam is _______________.
A thin prism is made of a material having refractive indices 1.61 and 1.65 for red and violet light. The dispersive power of the material is 0.07. It is found that a beam of yellow light passing through the prism suffers a minimum deviation of 4.0° in favourable conditions. Calculate the angle of the prism.
A thin prism of crown glass (μr = 1.515, μv = 1.525) and a thin prism of flint glass (μr = 1.612, μv = 1.632) are placed in contact with each other. Their refracting angles are 5.0° each and are similarly directed. Calculate the angular dispersion produced by the combination.
The refractive index of a material M1 changes by 0.014 and that of another material M2 changes by 0.024 as the colour of the light is changed from red to violet. Two thin prisms, one made of M1(A = 5.3°) and the other made of M2(A = 3.7°) are combined with their refracting angles oppositely directed. (a) Find the angular dispersion produced by the combination. (b) The prisms are now combined with their refracting angles similarly directed. Find the angular dispersion produced by the combination.
A ray of light is incident on a prism whose refractive index is 1.52 at an angle of 40°. If the angle of emergence is 60°, calculate the angle of the prism.
Prove that in case of a prism, i + e = A + δ, where the symbols have their usual meanings.
What is meant by a thin prism?
