Advertisements
Advertisements
Question
Find area of the ellipse `x^2/5^2 + y^2/4^2` = 1
Solution
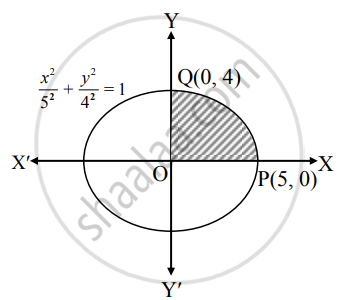
By the symmetry of the ellipse, required area of the ellipse is 4 times the area of the region OPQO.
For the region OPQO, the limits of integration are x = 0 and x = 5.
Given equation of the ellipse is `x^2/5^2 + y^2/4^2` = 1
∴ `y^2/4^2 = 1 - x^2/5^2`
∴ y2 = `4^2(1 - x^2/5^2) = 4^2/5^2(5^2 - x^2)`
∴ y = `+- 4/5 sqrt(5^2 - x^2)`
∴ y = `4/5 sqrt(5^2 - x^2)` ......[∵ In first quadrant, y > 0]
∴ Required area = 4(area of the region OPQO)
∴ `4 int_0^5 y "d"x = 4int_0^5 4/5 sqrt(5^2 - x^2) "d"x`
= `(4 xx 4)/5 int_0^5 sqrt((5)^2 - x^2) "d"x`
= `16/5[x/2 sqrt((5)^2 - x^2) + (5)^2/2 sin^-1 (x/5)]_0^5`
= `16/5 {[5/2 sqrt((5)^2 - (5)^2) + (5)^2/2 sin^-1 (5/5)] - [0/2 sqrt((5)^2 - 0^2) + (5)^2/2 sin^-1 (0/5)]}`
= `16/5 [0 + 25/2 sin^-1 (1) - (0 + 0)]`
= `16/5 (25/2 xx pi/2)`
= 20π sq.units
APPEARS IN
RELATED QUESTIONS
Find the area of the ellipse `x^2/4 + y^2/25 = 1`
Find the area of ellipse `x^2/(4) + y^2/(25)` = 1.
Using definite integration, the area of the circle x2 + y2 = 25 is ______.
Solve the following :
Find the area of the ellipse `x^2/(16) + y^2/(9)` = 1.
State whether the following statement is True or False:
The equation of the area of the ellipse is x2 + y2 = a2
Find area of the ellipse 4x2 + 9y2 = 36
