Advertisements
Advertisements
Question
Find the curved surface area of a cone with base radius 5.25 cm and slant height 10cm.
Solution
Given that,
Radius of a base of a cone = 5.25 cm
Slant height of cone=10 cm
Curved surface area of cone=` pirl`
`=22/7xx5.25xx10cm^2`
` =(22xx0.75xx10)cm^2`
`= 165 cm^2`
Thus, the curved surface area of a cone is `165cm^2`
APPEARS IN
RELATED QUESTIONS
A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is ₹ 12 per m2, what will be the cost of painting all these cones?
`("Use "π = 3.14" and take "sqrt1.04= 1.02)`
The height of a cone is 21 cm. Find the area of the base if the slant height is 28 cm.
Find the total surface area of a right circular cone with radius 6 cm and height 8 cm.
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of Rs. 210 per l00 m2.
A heap of wheat is in the form of a cone of diameter 16.8 m and height 3.5 m. Find its volume. How much cloth is required to just cover the heap?
A solid sphere and a solid hemi-sphere have the same total surface area. Find the ratio between their volumes.
A solid metallic cone, with radius 6 cm and height 10 cm, is made of some heavy metal A. In order to reduce its weight, a conical hole is made in the cone as shown and it is completely filled with a lighter metal B. The conical hole has a diameter of 6 cm and depth 4 cm. Calculate the ratio of the volume of metal A to the volume of the metal B in the solid.
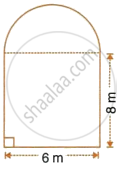
The cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle as shown in the figure. The tunnel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs. 2.25 per m2.
The curved surface area of a cone is 2200 sq.cm and its slant height is 50 cm. Find the total surface area of cone. `(π = 22/7)`
A right-angled triangle PQR where ∠Q = 90° is rotated about QR and PQ. If QR = 16 cm and PR = 20 cm, compare the curved surface areas of the right circular cones so formed by the triangle
