Advertisements
Advertisements
Question
Find the mutual inductance between the straight wire and the square loop of figure.
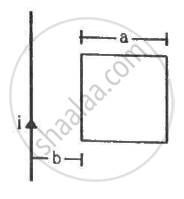
Solution
The flux through the square frame is given by `phi=Mi`
Let us first calculate the flux through the square frame.
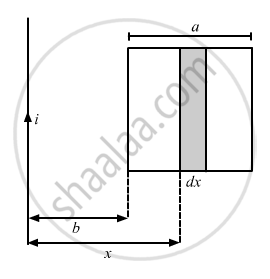
Let us now consider an element of loop of length dx at a distance x from the wire.
Now,
Area of the element of loop, A = adx
Magnetic field at a distance x from the wire,
\[B = \frac{\mu_0 i}{2\pi x}\]
The magnetic flux of the element is given by
\[d\phi = \frac{\mu_0 i \times adx}{2\pi x}\]
The total flux through the frame is given by
\[\phi = \int d\phi\]
\[ = \int_b^{a + b} \frac{\mu_0 iadx}{2\pi x}\]
\[ = \frac{\mu_0 ia}{2\pi}\ln\left[ 1 + \frac{a}{b} \right]\]
Also,
\[\phi = Mi\]
Thus, the mutual inductance is calculated as
\[Mi = \frac{\mu_0 ia}{2\pi}\ln\left[ 1 + \frac{a}{b} \right]\]
\[ \Rightarrow M = \frac{\mu_0 a}{2\pi}\ln\left[ 1 + \frac{a}{b} \right]\]
APPEARS IN
RELATED QUESTIONS
Define mutual inductance.
The current flowing through an inductor of self inductance L is continuously increasing. Plot a graph showing the variation of Magnetic potential energy stored versus the current.
Define coefficient of mutual induction.
Consider two concentric circular coils, one of radius r1 and the other of radius r2 (r1 < r2) placed coaxially with centers coinciding with each other. Obtain the expression for the mutual inductance of the arrangement.
Two circular loops are placed with their centres separated by a fixed distance. How would you orient the loops to have (a) the largest mutual inductance (b) the smallest mutual inductance?
An emf of 96.0 mV is induced in the windings of a coil when the current in a nearby coil is increasing at the rate of 1.20 A/s. What is the mutual inductance (M) of the two coils?
In an induction coil, the coefficient of mutual inductance is 6 henry. If a current of 10 ampere in the primary coil is cut-off in `1/1500"s"`, the e.m.f. at the terminals of the secondary coil will be ____________.
A current I = 10 sin (50 π t) ampere is passed in the first coil which induces a maximum e.m.f. of 5 π volt in the second coil. The mutual inductance between the coils is ______.
Two coils P and Q have mutual inductance 'M' H. If the current in the primary is I = I0 sin `omega`t, then the maximum vlaue of e.m.f. indued in coil Q is ____________.
A solenoid is connected to a battery so that a steady current flows through it. If an iron core is inserted into the solenoid, the current will ______.
If number of turns in primary and secondary coils is increased to two times each, the mutual inductance ______.
There are two coils A and B seperated by some distance. If a current of 2A flows through A, a magnetic flux of 10-2 Wb passes through B (no current through B). If no current passes through A and a current of 1A passes through B, what is the flux through A?
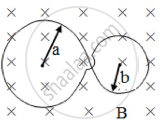
A plane loop is shaped in the form as shown in figure with radii a = 20 cm and b = 10 cm and is placed in a uniform time varying magnetic field B = B0 sin ωt, where B0 = 10 mT and ω = 100 rad/s. The amplitude of the current induced in the loop if its resistance per unit length is equal to 50 × 10-3 Ω/m. The inductance of the loop is negligible is ______ A.
Write the S.I. unit of mutual inductance.
A rectangular coil of wire 50 turn each of area 6 x 10-4 m2 is freely suspended in a field of 3 x 10-2 Wb / m2. Calculate the current flowing through the coil when it deflects through 60°, when torsional constant is 3.82 x 10-6 SI unit.
State and define the SI unit of mutual inductance.
Two coils having self inductances L1 = 75 mH and L2 = 55 mH are coupled with each other. The coefficient of coupling (K) is 0. 75. Calculate the mutual inductance (M) of the two coils
