Advertisements
Advertisements
Question
Consider two concentric circular coils, one of radius r1 and the other of radius r2 (r1 < r2) placed coaxially with centers coinciding with each other. Obtain the expression for the mutual inductance of the arrangement.
Solution

Coefficient of mutual induction − consider two coils P and S. Suppose that a current I is flowing through the coil P at any instant i.e.,
Φ ∝ I
Φ = MI… (i)
If ‘e’ is the induced emf produced in the S-coil, then
`e=(dphi)/dt=-d/dt(MI)=-M(dl)/dt`
Mutual Inductance of two concentric coils, one of radius r1 and the other of radius r2 (r1 < r2) placed coaxially with centers coinciding with each other:

Consider two circular coil S1 and S2 of same length l, such that coil S2 surrounds coil S1 completely
Let
n1 − Number of turns per unit length of S1
n2 − Number of turns per unit length of S2
I1 − Current passed through solenoid S1
Φ21 − Flux linked with S2 due to current flowing through S1
Φ21 ∝ I1
Φ21 = M21I1
Where M21 is the coefficient of mutual induction of the two coils
When current is passed through S1, an emf is induced in S2.
Magnetic field produced inside S1 on passing current through it,
B1 = μ0n1I1
Magnetic flux linked with each turn of S2 will be equal to B1 times the area of the cross-section of S1.
Magnetic flux linked with each turn of the S2 = B1A
Therefore, total magnetic flux linked with the S2,
Φ21 = B1A × n2l = μ0n1I1 × A× n2l
Φ21 = μ0n1n2AlI1
∴ M21 = μ0n1n2Al
Similarly, the mutual inductance between the two coils, when current is passed through coil S2 and induced emf is produced in coil S1, is given by
M12 = μ0n1n2Al
∴M12 = M21 = M (say)
Hence, coefficient of mutual induction between the two coil will be
|
`M=mu_0n_1n_2Al` |
APPEARS IN
RELATED QUESTIONS
In an experiment, two coils c1 and c2 are placed close to each other. Find out the expression for the emf induced in the coil c1 due to a change in the current through the coil c2.
The current flowing through an inductor of self inductance L is continuously increasing. Plot a graph showing the variation of Magnetic potential energy stored versus the current.
A 1.0 m long metallic rod is rotated with an angular frequency of 400 rad s−1 about an axis normal to the rod passing through its one end. The other end of the rod is in contact with a circular metallic ring. A constant and uniform magnetic field of 0.5 T parallel to the axis exists everywhere. Calculate the emf developed between the centre and the ring.
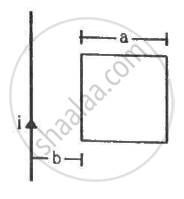
Find the mutual inductance between the straight wire and the square loop of figure.
A solenoid of length 20 cm, area of cross-section 4.0 cm2 and having 4000 turns is placed inside another solenoid of 2000 turns having a cross-sectional area 8.0 cm2 and length 10 cm. Find the mutual inductance between the solenoids.
Define Mutual Inductance.
Two different wire loops are concentric and lie in the same plane. The current in the outer loop (I) is clockwise and increases with time. The induced current in the inner loop.
The mutual inductance of a pair of coils is 0.75 H. If current in the primary coil changes from 0.5 A to zero in 0.01 s, find average induced e.m.f. in secondary coil ______.
Two circular coils have their centres at the same point. The mutual inductance between them will be maximum when their axes ______
The mutual inductance M12 of coil 1 with respect to coil 2 ______.
- increases when they are brought nearer.
- depends on the current passing through the coils.
- increases when one of them is rotated about an axis.
- is the same as M21 of coil 2 with respect to coil 1.
