Advertisements
Advertisements
Question
Find the amount of water displaced by a solid spherical ball of diameter 4.2 cm, when it is completely immersed in water.
Solution
Given: Diameter of spherical ball = 4.2 cm
Now, radius of spherical ball (r) = `4.2/2` cm = 2.1 cm
Amount of water displaced by solid spherical ball = Volume of solid spherical ball
So, volume of spherical ball = `4/3 pir^3`
= `4/3 xx 22/7 xx (2.1)^3`
= `88/21 xx 21/10 xx 21/10 xx 21/10`
= 38.808 cm3
Therefore, the amount of water displaced by solid spherical ball when it completed immersed in water is 38.808 cm3.
APPEARS IN
RELATED QUESTIONS
Twenty seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S'. Find the
- radius r' of the new sphere,
- ratio of S and S'.
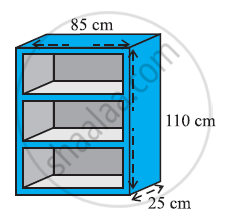
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm (see the given figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.
Find the volume of a sphere whose diameter is 3.5 dm .
A shopkeeper has one laddoo of radius 5 cm. With the same material, how many laddoos of radius 2.5 cm can be made?
If the radius of a sphere is doubled, what is the ratio of the volume of the first sphere to that of the second sphere?
A measuring jar of internal diameter 10 cm is partially filled with water. Four equal spherical balls of diameter 2 cm each are dropped in it and they sink down in water completely. What will be the change in the level of water in the jar?
The radius of the internal and external surfaces of a hollow spherical shell are 3 cm and 5 cm respectively. If it is melted and recast into a solid cylinder of heigh2`2/3`cm Find the diameter of the cylinder.
A hemisphere of lead of radius 7 cm is cast into a right circular cone of height 49 cm. Find the radius of the base.
The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
Metal spheres, each of radius 2 cm, are packed into a rectangular box of internal dimensions 16 cm × 8 cm × 8 cm. When 16 spheres are packed the box is filled with preservative liquid. Find the volume of this liquid. Give your answer to the nearest integer. [Use π = 3.14]
