Advertisements
Advertisements
Question
Twenty seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S'. Find the
- radius r' of the new sphere,
- ratio of S and S'.
Solution
(i) Radius of 1 solid iron sphere = r
The volume of 1 solid iron sphere = `4/3pir^3`
Volume of 27 solid iron spheres = `27xx4/3pir^3`
27 solid iron spheres are melted to form 1 iron sphere. Therefore, the volume of this iron sphere will be equal to the volume of 27 solid iron spheres. Let the radius of this new sphere be r'.
Volume of new solid iron sphere = `4/3pi(r"'")^3`
`4/3pi(r"'")^3` = `27xx4/3pir^3`
(r')3 = 27r3
r' = 3r
(ii) Surface area of 1 solid iron sphere of radius r = 4πr2
The surface area of iron sphere of radius r' = 4π (r')2
= 4 π (3r)2 = 36 πr2
`S/(S"'")` = `(4pir^2)/(36pir^2)`
= `1/9`
= 1 : 9
APPEARS IN
RELATED QUESTIONS
How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold?
`["Assume "pi=22/7]`
The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
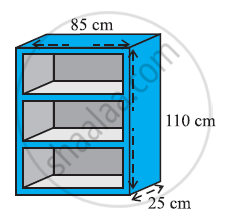
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm (see the given figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.
Find the volume of a sphere whose radius is 10.5 cm .
Find the volume of a sphere whose diameter is 14 cm .
A measuring jar of internal diameter 10 cm is partially filled with water. Four equal spherical balls of diameter 2 cm each are dropped in it and they sink down in water completely. What will be the change in the level of water in the jar?
The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
A sphere, a cylinder and a cone have the same diameter. The height of the cylinder and also the cone are equal to the diameter of the sphere. Find the ratio of their volumes.
A solid sphere and a solid hemisphere have an equal total surface area. Prove that the ratio of their volume is `3sqrt(3):4`
A hemispherical tank of radius 1.75 m is full of water. It is connected with a pipe which empties the tank at the rate of 7 litres per second. How much time will it take to empty the tank completely?
