Question

Find the central angle of the shaded sectors (each circle is divided into equal sectors).

Sectors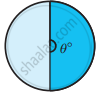
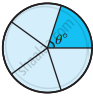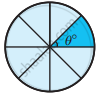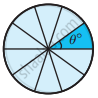Central angle of each sector (θ°)

Answer 1

Sectors
Central angle of each sector (θ°)	Number of equal parts n = 2 θ° = `(360^circ)/"n" = (360^circ)/2` θ° = 180°	Number of equal parts n = 5 θ° = `(360^circ)/"n"` θ° = `(360^circ)/2` θ° = 72°	Number of equal parts n = 8 θ° = `(360^circ)/"n"` θ° = `(360^circ)/8` θ° = 45°	Number of equal parts n = 10 θ° = `(360^circ)/"n"` θ° = `(360^circ)/10` θ° = 36°