Advertisements
Advertisements
Question
Find the diameter of a circle whose circumference is equal to the sum of circumference of circles with radius 10 cm, 12 cm, and 18 cm.
Solution
Let the radius of the circle = R cm
∴ 2πR = 2π × 10 + 2π × 12 + 2π × 18
On dividing each term by 2π, we get:
R = 10 + 12 + 18 = 40 cm
∴ Radius of the circle obtained = 40 cm
And, its diameter = 2 × Radius
= 2 × 40 cm = 80 cm
APPEARS IN
RELATED QUESTIONS
The hypotenuse of a right-angled triangle is 65 cm and its base is 60 cm. Find the length of perpendicular and the area of the triangle.
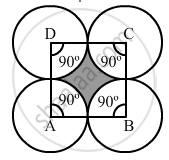
Four equal circles are described about the four corners of a square so that each touches two of the others, as shown in the figure. Find the area of the shaded region, if each side of the square measures 14 cm.
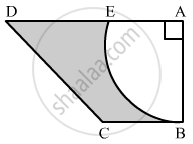
In the given figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region.
PQRS is a diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal. Semicircles are drawn with PQ and QS as diameters, as shown in the given figure. If PS = 12 cm, find the perimeter and area of the shaded region.
The area of the circle is given below; find the diameter.
176 sq cm
Find the area enclosed between two concentric circles, if their radii are 6 cm and 13 cm respectively.
A lawn is in the shape of a semi-circle of diameter 42 m. The lawn is surrounded by a flower bed of width 7 m all around. Find the area of the flower bed in m2 .
Find the area and perimeter of the following sector :
Diameter = 42 cm, angle at the centre is 100·.
A wire is bent to form a square of side 22 cm. If the wire is rebent to form a circle, its radius is ______.
Area of circular garden with diameter 8 m is ______.
