Advertisements
Advertisements
Question
Find the area and perimeter of the following sector :
Diameter = 42 cm, angle at the centre is 100·.
Solution
Diameter= 2r
`=> "r" = "diameter" /2 = 42/2 = 21 "cm"`
Area of the sector = `(pi "r"^2 xx theta/360^circ)`
`= 22/7 xx 21 xx 21 xx 100^circ/360^circ`
= 385 cm2
Peri meter of the sector = `2"r" + (2 pi "r" xx theta /360^circ)`
`= 2 xx 21 + (2 xx 22/7 xx 21 xx 100^circ/360^circ)`
= 42 + 36.66
= 78.66 cm
Area of the sector = 385 cm2 and perimeter = 78.66 cm
APPEARS IN
RELATED QUESTIONS
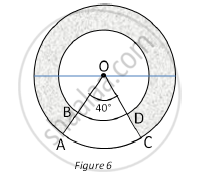
In Fig. 6, find the area of the shaded region, enclosed between two concentric circles of radii 7 cm and 14 cm where ∠AOC = 40°. (use `pi = 22/7`)
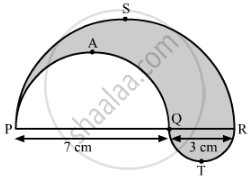
In PSR, RTQ and PAQ are three semicircles of diameters 10 cm, 3 cm and 7 cm respectively. Find the perimeter of the shaded region. [Use π=3.14]
A bicycle whell makes 5000 revolutions in moving 11 km. Find the diameter of the wheel
A car has wheels which are 80 cm in diameter. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour ?
A road which is 7m wide surrounds a circular park whose circumference is 352m. Find the area of road.
The radii of two circles are 19 cm and 9 cm, Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the areas of the minor major segments.
The side of a square is 10 cm. Find the area of the circumscribed circle. [π = 3.14]
The radius of a circular garden is 100 m. There is a road 10 m wide, running all around it. Find the area of the road and the cost of levelling it at Rs 20 per m2. [Use π = 3.14]
The difference between the circumference and radius of a circle is 37 cm. The area of the circle is
Find the area and perimeter of the circle with the following :
Radius= 2.8 cm
Find the diameter of the sphere for the following :
Surface Area = 221. 76 cm2
The radii of two circles are 48 cm and 13 cm. Find the area of the circle which has its circumference equal to the difference of the circumferences of the given two circles.
The radius of two circles are 20 cm and 13 cm. Find the difference between their circumferences. (Take π =`22/7`)
The circumferences of two circles are in the ratio 5: 7, find the ratio between their radius.
Construct an angle PQR = 45°. Mark a point S on QR such that QS = 4.5 cm. Construct a circle to touch PQ at Q and also to pass through S.
Find the number of revolutions made by a circular wheel of area 1.54 m2 in rolling a distance of 176 m.
Circumference ‘C’ of a circle is equal to 2π × ______.
Ratio of circumference of a circle to its radius is always 2π:I.
