Advertisements
Advertisements
Question
Find the direction ratios of the normal to the plane 2x + 3y + z = 7
Solution
The direction ratios of the normal to the plane 2x + 3y + z = 7 are 2, 3, 1.
APPEARS IN
RELATED QUESTIONS
Find the vector equation of a plane which is at 42 unit distance from the origin and which is normal to the vector `2hati + hatj - 2hatk`.
Reduce the equation `bar"r".(3hat"i" + 4hat"j" + 12hat"k")` to normal form and hence find
(i) the length of the perpendicular from the origin to the plane
(ii) direction cosines of the normal.
Find the vector equation of the plane passing through the point having position vector `hati + hatj + hatk` and perpendicular to the vector `4hati + 5hatj + 6hatk`.
Show that the line `bar"r" = (2hat"j" - 3hat"k") + lambda(hat"i" + 2hat"j" + 3hat"k") and bar"r" = (2hat"i" + 6hat"j" + 3hat"k") + mu(2hat"i" + 3hat"j" + 4hat"k")` are coplanar. Find the equation of the plane determined by them.
Choose correct alternatives :
The length of the perpendicular from (1, 6,3) to the line `x/(1) = (y - 1)/(2) =(z - 2)/(3)`
Choose correct alternatives :
The lines `x/(1) = y/(2) = z/(3) and (x - 1)/(-2) = (y - 2)/(-4) = (z - 3)/(6)` are
The perpendicular distance of the plane 2x + 3y – z = k from the origin is `sqrt(14)` units, the value of k is ______.
Choose correct alternatives :
The equation of the plane passing through the points (1, −1, 1), (3, 2, 4) and parallel to the Y-axis is ______
Choose correct alternatives :
The equation of the plane in which the line `(x - 5)/(4) = (y - 7)/(4) = (z + 3)/(-5) and (x - 8)/(7) = (y - 4)/(1) = (z - 5)/(3)` lie, is
Find direction cosines of the normal to the plane `bar"r"*(3hat"i" + 4hat"k")` = 5
Find the vector equation of the plane which bisects the segment joining A(2, 3, 6) and B(4, 3, −2) at right angles
If z1 and z2 are z-coordinates of the points of trisection of the segment joining the points A (2, 1, 4), B (–1, 3, 6) then z1 + z2 = ______.
The equation of a plane containing the point (1, - 1, 2) and perpendicular to the planes 2x + 3y - 2z = 5 and x + 2y - 3z = 8 is ______.
If the line `(x - 3)/2 = (y + 2)/-1 = (z + 4)/3` lies in the plane lx + my - z = 9, then l2 + m2 is equal to ______
Equation of the plane passing through A(-2, 2, 2), B(2, -2, -2) and perpendicular to x + 2y - 3z = 7 is ______
If line `(2x - 4)/lambda = ("y" - 1)/2 = ("z" - 3)/1` and `(x - 1)/1 = (3"y" - 1)/lambda = ("z" - 2)/1` are perpendicular to each other then λ = ______.
The equation of the plane through (1, 2, -3) and (2, -2, 1) and parallel to the X-axis is ______
Equation of the plane perpendicular to the line `x/1 = y/2 = z/3` and passing through the point (2, 3, 4) is ______
The equation of the plane through the point (2, -1, -3) and parallel to the lines `(x - 1)/3 = (y + 2)/2 = z/(-4)` and `x/2 = (y - 1)/(-3) = (z - 2)/2` is ______
The equation of the plane, which bisects the line joining the points (1, 2, 3) and (3, 4, 5) at right angles is ______
If the plane passing through the points (1, 2, 3), (2, 3, 1) and (3, 1, 2) is ax + by + cz = d then a + 2b + 3c = ______.
The equation of the plane passing through the intersection of the planes x + 2y + 3z + 4 = 0 and 4x + 3y + 2z + 1 = 0 and the origin is ______.
Let the line `(x - 2)/3 = (y - 1)/(-5) = (z + 2)/2` lie in the plane x + 3y - αz + β = 0. Then, (α, β) equals ______
The equation of the plane passing through the points (1, –2, 1), (2, –1, –3) and (0, 1, 5) is ______.
The equation of the plane passing through a point having position vector`-2hat"i" + 7hat"j" + 5hat"k"` and parallel to the vectors `4hat"i" - hat"j" + 3hat"k"` and `hat"i" + hat"j" + hat"k"` is ______.
Find the vector equation of the plane passing through the point A(–1, 2, –5) and parallel to the vectors `4hati - hatj + 3hatk` and `hati + hatj - hatk`.
Let P be a plane Ix + my + nz = 0 containing the line, `(1 - x)/1 = ("y" + 4)/2 = ("z" + 2)/3`. If plane P divides the line segment AB joining points A(–3, –6, 1) and B(2, 4, –3) in ratio k:1 then the value of k is equal to ______.
If the foot of the perpendicular drawn from the origin to the plane is (4, –2, 5), then the equation of the plane is ______.
Find the equation of the plane containing the lines `(x - 1)/2 = (y + 1)/-1 = z/3` and `x/2 = (y - 2)/-1 = (z + 1)/3`.
Find the equation of plane which is at a distance of 4 units from the origin and which is normal to the vector `2hati - 2hatj + hatk`.
The coordinates of the foot of the perpendicular from the point P(1, 0, 0) in the line `(x - 1)/2 = (y + 1)/-3 = (z + 10)/8` are ______.
Find the vector equation of the line passing through the point (–2, 1, 4) and perpendicular to the plane `barr*(4hati - 5hatj + 7hatk)` = 15
A mobile tower is situated at the top of a hill. Consider the surface on which the tower stands as a plane having points A(1, 0, 2), B(3, –1, 1) and C(1, 2, 1) on it. The mobile tower is tied with three cables from the points A, B and C such that it stands vertically on the ground. The top of the tower is at point P(2, 3, 1) as shown in the figure below. The foot of the perpendicular from the point P on the plane is at the point `Q(43/29, 77/29, 9/29)`.
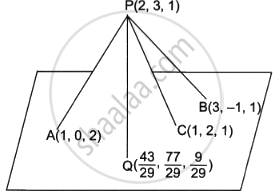
Answer the following questions.
- Find the equation of the plane containing the points A, B and C.
- Find the equation of the line PQ.
- Calculate the height of the tower.
