Advertisements
Advertisements
Question
A mobile tower is situated at the top of a hill. Consider the surface on which the tower stands as a plane having points A(1, 0, 2), B(3, –1, 1) and C(1, 2, 1) on it. The mobile tower is tied with three cables from the points A, B and C such that it stands vertically on the ground. The top of the tower is at point P(2, 3, 1) as shown in the figure below. The foot of the perpendicular from the point P on the plane is at the point `Q(43/29, 77/29, 9/29)`.
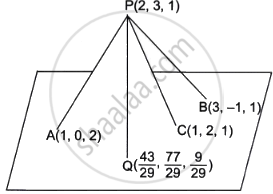
Answer the following questions.
- Find the equation of the plane containing the points A, B and C.
- Find the equation of the line PQ.
- Calculate the height of the tower.
Solution
i. A(1, 0, 2), B(3, –1, 1), C(1, 2, 1)
Equation of plane
`|(x - x_1, y - y_1, z - z_1),(x_2 - x_1, y_2 - y_1, z_2 - z_1),(x_3 - x_1, y_3 - y_1, z_3 - z_1)| = 0`
`\implies |(x - 1, y - 0, z - 2),(3 - 1, -1 - 0, 1 - 2),(1 - 1, 2 - 0, 1 - 2)| = 0`
`\implies |(x - 1, y - 0, z - 2),(2, -1, -1),(0, 2, -1)| = 0`
`\implies` (x – 1)(1 + 2) – y(–2 – 0) + (z – 2)(4 – 0) = 0
`\implies` 3(x – 1) + 2y + 4(z – 2) = 0
`\implies` 3x – 3 + 2y + 4z – 8 = 0
`\implies` 3x + 2y + 4z = 11
ii. Let a and b be the position vectors of the points P(2, 3, 1) and `Q(43/29, 77/29, 9/29)` respectively.
Then, `veca = 2hati + 3hatj + hatk` and `vecb = 43/29hati + 77/29hatj + 9/29hatk`
Let `vecr` represent the position vector of any point A(x, y, z) on the line connecting points P and Q. The vector equation for the line is
`vecr = veca + λ(vecb - veca)`
= `(2hati + 3hatj + hatk) + λ[(43/29 - 2)hati + (77/29 - 3)hatj + (9/29 - 1)hatk]`
= `(2hati + 3hatj + hatk) + λ[((-15)/29)hati + ((-10)/29)hatj + ((-20)/29)hatk]`
Where λ is a parameter.
iii. The coordinates of the point P(2, 3, 1) and the equation of the plane in which the tower's bottom is located are 3x + 2y + 4z = 11.
Height of tower = `|(3(2) + 2(3) + 4(1) - 11)/sqrt(3^2 + 2^2 + 4^2)|`
= `|(6 + 6 + 4 - 11)/sqrt(9 + 4 + 16)|`
= `5/sqrt(29)`
APPEARS IN
RELATED QUESTIONS
Find the coordinates of the foot of the perpendicular drawn from the origin to the plane 2x + 6y – 3z = 63.
Choose correct alternatives :
The equation of the plane passing through (2, -1, 3) and making equal intercepts on the coordinate axes is
Choose correct alternatives :
The equation of the plane passing through the points (1, −1, 1), (3, 2, 4) and parallel to the Y-axis is ______
Choose correct alternatives :
The equation of the plane in which the line `(x - 5)/(4) = (y - 7)/(4) = (z + 3)/(-5) and (x - 8)/(7) = (y - 4)/(1) = (z - 5)/(3)` lie, is
Choose correct alternatives :
The foot of perpendicular drawn from the point (0,0,0) to the plane is (4, -2, -5) then the equation of the plane is
Solve the following :
Find the coordinates of the foot of the perpendicular drawn from the origin to the plane 2x + 3y + 6z = 49.
Solve the following :
Reduce the equation `bar"r".(6hat"i" + 8hat"j" + 24hat"k")` = 13 normal form and hence find
(i) the length of the perpendicular from the origin to the plane.
(ii) direction cosines of the normal.
The equation of X axis is ______
Find direction cosines of the normal to the plane `bar"r"*(3hat"i" + 4hat"k")` = 5
Find the perpendicular distance of origin from the plane 6x − 2y + 3z - 7 = 0
Show that the lines `(x + 1)/(-10) = (y + 3)/(-1) = (z - 4)/(1)` and `(x + 10)/(-1) = (y + 1)/(-3) = (z - 1)/4` intersect each other.also find the coordinates of the point of intersection
Find the vector equation of the plane which bisects the segment joining A(2, 3, 6) and B(4, 3, −2) at right angles
The equation of a plane containing the point (1, - 1, 2) and perpendicular to the planes 2x + 3y - 2z = 5 and x + 2y - 3z = 8 is ______.
If 0 ≤ x < 2π, then the number of real values of x, which satisfy the equation cos x + cos 2x + cos 3x + cos 4x = 0, is ______
Equations of planes parallel to the plane x - 2y + 2z + 4 = 0 which are at a distance of one unit from the point (1, 2, 3) are _______.
If line `(2x - 4)/lambda = ("y" - 1)/2 = ("z" - 3)/1` and `(x - 1)/1 = (3"y" - 1)/lambda = ("z" - 2)/1` are perpendicular to each other then λ = ______.
Equation of the plane perpendicular to the line `x/1 = y/2 = z/3` and passing through the point (2, 3, 4) is ______
The equation of the plane, which bisects the line joining the points (1, 2, 3) and (3, 4, 5) at right angles is ______
The distance of the point (1, 0, 2) from the point of intersection of the line `(x - 2)/3 = (y + 1)/4 = (z - 2)/12` and the plane x - y + z = 16, is ______
If the plane passing through the points (1, 2, 3), (2, 3, 1) and (3, 1, 2) is ax + by + cz = d then a + 2b + 3c = ______.
If the plane x - 3y + 5z = d passes through the point (1, 2, 4), then the lengths of intercepts cut by it on the axes of X, Y, Z are respectively ______
If the mirror image of the point (2, 4, 7) in the plane 3x – y + 4z = 2 is (a, b, c), then 2a + b + 2c is equal to ______.
Let Q be the mirror image of the point P(1, 2, 1) with respect to the plane x + 2y + 2z = 16. Let T be a plane passing through the point Q and contains the line `vecr = -hatk + λ(hati + hatj + 2hatk)`, λ ∈ R. Then, which of the following points lies on T?
The coordinates of the foot of the perpendicular from the point P(1, 0, 0) in the line `(x - 1)/2 = (y + 1)/-3 = (z + 10)/8` are ______.
Find the vector equation of the line passing through the point (–2, 1, 4) and perpendicular to the plane `barr*(4hati - 5hatj + 7hatk)` = 15
Find the point of intersection of the line `(x + 1)/2 = (y - 1)/3 = (z - 2)/1` with the plane x + 2y – z = 6.
Find the equation of the plane containing the line `x/(-2) = (y - 1)/3 = (1 - z)/1` and the point (–1, 0, 2).
