Advertisements
Advertisements
Question
Find the equation of the circle with centre on the X-axis and passing through the origin having radius 4.
Solution
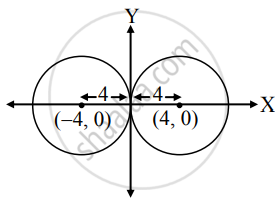
Let the co-ordinates of the centre of the required circle be C(h, 0).
Since the circle passes through the origin i.e., O(0,0),
OC = radius
∴ `sqrt(("h" - 0)^2 + (0 - 0)^2` = 4
∴ h2 = 16
∴ h = ± 4
∴ the co-ordinates of the centre are (4, 0) or (– 4, 0).
The equation of a circle with centre at (h, k) and radius r is given by
(x – h)2 + (y – k)2 = r2
Here, h = ± 4, k = 0, r = 4
∴ The required equation of the circle is
(x – 4)2 + (y – 0)2 = 42 or (x + 4)2 + (y – 0)2 = 42
∴ x2 – 8x + 16 + y2 = 16 or x2 + 8x + 16 + y2 = 16
∴ x2 + y2 – 8x = 0 or x2 + y2 + 8x = 0
APPEARS IN
RELATED QUESTIONS
Find the equation of the circle with centre at origin and radius 4.
Find the equation of the circle with centre at (−3, −2) and radius 6.
Find the equation of the circle with centre at (2, −3) and radius 5.
Find the equation of the circle with centre at (−3, −3) passing through the point (−3, −6)
Find the centre and radius of the circle:
(x − 5)2 + (y − 3)2 = 20
Find the equation of the circle with centre at (–2, 3) touching the X-axis.
Find the equation circle if the equations of two diameters are 2x + y = 6 and 3x + 2y = 4. When radius of circle is 9
Find the equation of circle (a) passing through the origin and having intercepts 4 and −5 on the co-ordinate axes
Find the centre and radius of the following:
x2 + y2 − 2x + 4y − 4 = 0
Find the centre and radius of the following:
x2 + y2 − 6x − 8y − 24 = 0
Show that the equation 3x2 + 3y2 + 12x + 18y − 11 = 0 represents a circle
Find the equation of the circle passing through the points (5, 7), (6, 6) and (2, −2)
Choose the correct alternative:
Equation of a circle which passes through (3, 6) and touches the axes is
Choose the correct alternative:
Find the equation of the circle which passes through the points (2, 3) and (4, 5) and the centre lies on the straight line y − 4x + 3 = 0
Choose the correct alternative:
If the lines 3x − 4y + 4 = 0 and 6x − 8y − 7 = 0 are tangents to a circle, then find the radius of the circle
Choose the correct alternative:
Area of the circle centre at (1, 2) and passing through (4, 6) is
Choose the correct alternative:
If a circle passes through the point (0, 0), (a, 0) and (0, b) then find the co-ordinates of its centre
Choose the correct alternative:
The equation of a circle with origin as centre and passing through the vertices of an equilateral triangle whose median is of length 3a is
Answer the following :
Find the equation of circle passing through the point of intersection of the lines x + 3y = 0 and 2x − 7y = 0 whose centre is the point of intersection of lines x + y + 1 = 0 and x − 2y + 4 = 0
Answer the following :
Find the equation of circle which passes through the origin and cuts of chords of length 4 and 6 on the positive side of x-axis and y-axis respectively
Answer the following :
Show that the points (9, 1), (7, 9), (−2, 12) and (6, 10) are concyclic
Answer the following :
Show that the circles touch each other externally. Find their point of contact and the equation of their common tangent:
x2 + y2 – 4x + 10y +20 = 0,
x2 + y2 + 8x – 6y – 24 = 0.
Answer the following :
Show that the circles touch each other externally. Find their point of contact and the equation of their common tangent:
x2 + y2 – 4x – 10y + 19 = 0,
x2 + y2 + 2x + 8y – 23 = 0.
Answer the following :
Show that the circles touch each other internally. Find their point of contact and the equation of their common tangent:
x2 + y2 – 4x – 4y – 28 = 0,
x2 + y2 – 4x – 12 = 0
Answer the following :
Show that the circles touch each other internally. Find their point of contact and the equation of their common tangent:
x2 + y2 + 4x – 12y + 4 = 0,
x2 + y2 – 2x – 4y + 4 = 0
The centre of the circle x = 3 + 5 cos θ, y = - 4 + 5 sin θ, is ______
If the radius of a circle increases from 3 cm to 3.2 cm, then the increase in the area of the circle is ______
The radius of a circle is increasing uniformly at the rate of 2.5cm/sec. The rate of increase in the area when the radius is 12cm, will be ______
If x2 + (2h - 1)xy + y2 - 24x - 8y + k = 0 is the equation of the circle and 12 is the radius of the circle, then ______.
Let AB be a chord of the circle x2 + y2 = r2 subtending a right angle at the centre, then the locus of the centroid of the ΔPAB as P moves on the circle is ______.
