Advertisements
Advertisements
Question
Find the G.C.D. of the given polynomials
3x4 + 6x3 – 12x2 – 24x, 4x4 + 14x3 + 8x2 – 8x
Solution
p(x) = 3x4 + 6x3 – 12x2 – 24x
= 3x (x3 + 2x2 – 4x – 8)
g(x) = 4x4 + 14x3 + 8x2 – 8x
= 2x (2x3 + 7x2 + 4x – 4)
G.C.D. of 3x and 2x = x
Now g(x) is divide by p(x) we get
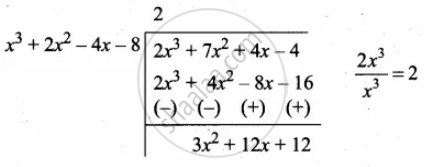
3x2 + 12x + 12 = 3 (x2 + 4x + 4)
Now dividing p(x) = x3 + 2x2 – 4x – 8
by the new remainder ...(leaving the constant)
x2 + 4x + 4

G.C.D. = x(x2 + 4x + 4) ...[Note x is common for p(x) and g(x)]
APPEARS IN
RELATED QUESTIONS
Find the G.C.D. of the given polynomials
3x3 + 3x2 + 3x + 3, 6x3 + 12x2 + 6x + 12
Find the L.C.M. of the given expressions
4x2y, 8x3y2
Find the L.C.M. of the given expressions
– 9a3b2, 12a2b2c
Find the L.C.M. of the given expressions
p2 – 3p + 2, p2 – 4
Find the L.C.M. of the given expressions
(2x2 – 3xy)2, (4x – 6y)3, (8x3 – 27y3)
Find the LCM and GCD for the following and verify that f(x) × g(x) = LCM × GCD
(x3 – 1) (x + 1), (x3 + 1)
Find the GCD pair of the following polynomials
(x3 + y3), (x4 + x2y2 + y4) whose LCM is (x3 + y3) (x2 + xy + y2)
Given the LCM and GCD of the two polynomials p(x) and q(x) find the unknown polynomial in the following table
| LCM | GCD | p(x) | q(x) |
| (x4 – y4)(x4 + x2y2 + y2) | (x2 – y2) | (x4 – y4)(x2 + y2 – xy) |
If (x – 6) is the HCF of x2 – 2x – 24 and x2 – kx – 6 then the value of k is
Find the least common multiple of xy(k2 + 1) + k(x2 + y2) and xy(k2 – 1) + k(x2 – y2)
