Advertisements
Advertisements
Question
Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
Solution
Let the image of P(3, 8) and P’(a, b)
Let the point of intersection be O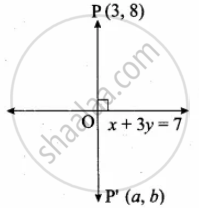
Slope of x + 3y = 7 is `-1/3`
Slope of PP’ = 3 ...(perpendicular)
Equation of PP’ is
y – y1 = m(x – x1)
y – 8 = 3(x – 3)
y – 8 = 3x – 9
– 8 + 9 = 3x – y
∴ 3x – y = 1 ...(1)
The two line meet at 0
x + 3y = 7 ...(2)
(1) × 3 ⇒ 9x – 3y = 3 ...(3)
(2) × 1 ⇒ x + 3y = 7 ...(4)
Adding (1) and (2) ⇒ 10x = 10
x = `10/10` = 1
Substitute the value of x = 1 in (1)
3 – y = 1
3 – 1 = y
2 = y
The point O is (1, 2)
Mid point of pp’ = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
(1, 2) = `((3 + "a")/2, (8 + "b")/2)`
∴ `(3 + "a")/2` = 1
⇒ 3 + a = 2
a = 2 – 3 = – 1
`(8 + "b")/2` = 2
8 + b = 4
b = 4 – 8 = – 4
The point P’ is (– 1, – 4)
APPEARS IN
RELATED QUESTIONS
Find the slope of the following straight line
5y – 3 = 0
Find the slope of the following straight line
`7x - 3/17` = 0
Check whether the given lines are parallel or perpendicular
`x/3 + y/4 + 1/7` = 0 and `(2x)/3 + y/2 + 1/10` = 0
Check whether the given lines are parallel or perpendicular
5x + 23y + 14 = 0 and 23x – 5x + 9 = 0
If the straight lines 12y = − (p + 3)x + 12, 12x – 7y = 16 are perpendicular then find ‘p’
Find the equation of a line passing through (6, −2) and perpendicular to the line joining the points (6, 7) and (2, −3)
Find the equation of a straight line through the intersection of lines 7x + 3y = 10, 5x – 4y = 1 and parallel to the line 13x + 5y + 12 = 0
Find the equation of a straight line through the point of intersection of the lines 8x + 3y = 18, 4x + 5y = 9 and bisecting the line segment joining the points (5, −4) and (−7, 6)
The equation of a line passing through the origin and perpendicular to the line 7x − 3y + 4 = 0 is
Consider four straight lines
(i) l1; 3y = 4x + 5
(ii) l2; 4y = 3x – 1
(iii) l3; 4y + 3x = 7
(iv) l4; 4x + 3y = 2
Which of the following statement is true?
