Advertisements
Advertisements
Question
Find the joint equation of the line which are at a distance of 9 units from the Y-axis.
Solution
Equations of the lines, which are parallel to the Y-axis and at a distance of 9 units from it, are x = 9 and x = - 9
i.e. x - 9 = 0 and x + 9 = 0
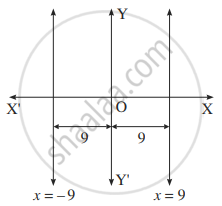
∴ their combined equation is
(x - 9)(x + 9) = 0
∴ x2 - 81 = 0
APPEARS IN
RELATED QUESTIONS
Find the combined equation of the following pair of line:
2x + y = 0 and 3x − y = 0
Find the combined equation of the following pair of line passing through (−1, 2), one is parallel to x + 3y − 1 = 0 and other is perpendicular to 2x − 3y − 1 = 0
Find the separate equation of the line represented by the following equation:
5x2 – 9y2 = 0
Find the separate equation of the line represented by the following equation:
x2 + 2xy tan α - y2 = 0
Find the combined equation of the pair of a line passing through the origin and perpendicular to the line represented by following equation:
5x2 - 8xy + 3y2 = 0
If the slope of one of the two lines given by `"x"^2/"a" + "2xy"/"h" + "y"^2/"b" = 0` is twice that of the other, then ab : h2 = ______.
Choose correct alternatives:
The combined equation of the coordinate axes is
Find the joint equation of the line:
x + y - 3 = 0 and 2x + y - 1 = 0
Find the joint equation of the line passing through the origin having slopes 2 and 3.
Find the joint equation of the line passing through the origin and having inclinations 60° and 120°.
Find the joint equation of the line passing through (1, 2) and parallel to the coordinate axes
Find the joint equation of the line passing through (-1, 2) and perpendicular to the lines x + 2y + 3 = 0 and 3x - 4y - 5 = 0
Show that the following equations represent a pair of line:
x2 - y2 = 0
Find the separate equation of the line represented by the following equation:
6x2 - 5xy - 6y2 = 0
Find the separate equation of the line represented by the following equation:
3x2 - y2 = 0
Find k, if the slope of one of the lines given by 3x2 + 4xy + ky2 = 0 is three times the other.
Find k, if one of the lines given by 6x2 + kxy + y2 = 0 is 2x + y = 0.
Find an if the sum of the slope of lines represented by ax2 + 8xy + 5y2 = 0 is twice their product.
If the lines given by ax2 + 2hxy + by2 = 0 form an equilateral triangle with the line lx + my = 1, show that (3a + b)(a + 3b) = 4h2.
If the line x + 2 = 0 coincides with one of the lines represented by the equation x2 + 2xy + 4y + k = 0, then prove that k = - 4.
Prove that the combined of the pair of lines passing through the origin and perpendicular to the lines ax2 + 2hxy + by2 = 0 is bx2 - 2hxy + ay2 = 0.
Find the joint equation of the line passing through the origin and having slopes 1 + `sqrt3` and 1 - `sqrt3`
The combined equation of the lines through origin and perpendicular to the pair of lines 3x2 + 4xy − 5y2 = 0 is ______
The joint equation of pair of lines through the origin, each of which makes an angle of 60° with Y-axis, is ______
The joint equation of the lines through the origin which forms two of the sides of the equilateral triangle having x = 2 as the third side is ______
The equation of line passing through the midpoint of the line joining the points (-1, 3, -2) and (-5, 3, -6) and equally inclined to the axes is ______.
The combined equation of the lines which pass through the origin and each of which makes an angle of 30° with the line 3x + 2y – 11 = 0 is ______.
The line 5x + y – 1 = 0 coincides with one of the lines given by 5x2 + xy – kx – 2y + 2 = 0 then the value of k is ______.
Find the combined equation of the pair of lines passing through the origin and perpendicular to the lines represented by 3x2 + 2xy – y2 = 0.
If `x^2/a + y^2/b + (2xy)/h` = 0 represents a pair of lines and slope of one line is twice the other, then find the value of ab : h2.
Combined equation of the lines bisecting the angles between the coordinate axes, is ______.
