Advertisements
Advertisements
Question
Find the ratio in which Y-axis divides the point A(3, 5) and point B(– 6, 7). Find the coordinates of the point
Solution
Let C be a point on Y-axis which divides seg AB in the ratio m : n
Point C lies on the Y-axis.
∴ its X-coordinate is 0.
Let C = (0, y)
Here,
A(x1, y1) = A(3, 5)
B(x2, y2) = B(– 6, 7)
By Section formula,
x =
∴ 0 =
∴ – 6m + 3n = 0
∴ 3n = 6m
∴
∴
∴ m : n = 1 : 2
By section formula,
y =
y =
=
=
=
∴ Y-axis divides the seg AB in the ratio 1 : 2 and the co-ordinates of that point is
APPEARS IN
RELATED QUESTIONS
Let P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
Find the coordinates of the point which divides the line segment joining the points (6, 3) and (– 4, 5) in the ratio 3 : 2 internally.
If the point C (–1, 2) divides internally the line segment joining A (2, 5) and B in ratio 3 : 4, find the coordinates of B
The three vertices of a parallelogram taken in order are (–1, 0), (3, 1) and (2, 2) respectively. Find the coordinates of the fourth vertex.
If the coordinates of the mid-points of the sides of a triangle are (1, 2) (0, –1) and (2, 1). Find the coordinates of its vertices.
If the coordinates of the mid points of the sides of a triangle are (1, 1), (2, – 3) and (3, 4) Find its centroid
If a vertex of a triangle be (1, 1) and the middle points of the sides through it be (-2,-3) and (5 2) find the other vertices.
Three vertices of a parallelogram are (a+b, a-b), (2a+b, 2a-b), (a-b, a+b). Find the fourth vertex.
If two vertices of a parallelogram are (3, 2) (-1, 0) and the diagonals cut at (2, -5), find the other vertices of the parallelogram.
In what ratio does the point (a, 6) divide the join of (–4, 3) and (2, 8)? Also, find the value of a.
A (–3, 4), B (3, –1) and C (–2, 4) are the vertices of a triangle ABC. Find the length of line segment AP, where point P lies inside BC, such that BP : PC = 2 : 3.
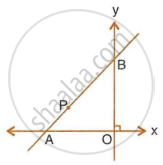
In the given figure, line APB meets the x-axis at point A and y-axis at point B. P is the point (−4, 2) and AP : PB = 1 : 2. Find the co-ordinates of A and B.
A(20, 0) and B(10, –20) are two fixed points. Find the co-ordinates of the point P in AB such that : 3PB = AB. Also, find the co-ordinates of some other point Q in AB such that : AB = 6 AQ.
Find the length of the hypotenuse of a square whose side is 16 cm.
Find the coordinate of a point P which divides the line segment joining :
A(-8, -5) and B (7, 10) in the ratio 2:3.
Find the ratio in which the line x = -2 divides the line segment joining (-6, -1) and (1, 6). Find the coordinates of the point of intersection.
The points (-5, 1), (1, p) and (4, -2) are collinear if the value of p is ______.
A line intersects the y-axis and x-axis at the points P and Q, respectively. If (2, –5) is the mid-point of PQ, then the coordinates of P and Q are, respectively ______.
Find the co-ordinates of the points of trisection of the line segment joining the points (5, 3) and (4, 5).
What is the ratio in which the line segment joining (2, -3) and (5, 6) is divided by x-axis?
