Advertisements
Advertisements
Question
For light diverging from a point source ______.
- the wavefront is spherical.
- the intensity decreases in proportion to the distance squared.
- the wavefront is parabolic.
- the intensity at the wavefront does not depend on the distance.
Options
a and b
a and c
b and c
c and d
Solution
a and b
Explanation:
| Type of wavefront | Intensity | Amplitude |
Spherical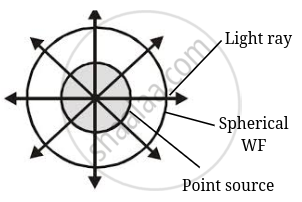 |
`I oo 1/r^2` | `A oo 1/r` |
Cylindrical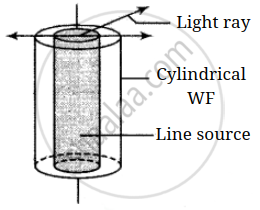 |
`I oo 1/r` | `A oo 1/sqrt(r)` |
Plane |
`I oo 1/r^0` | `A oo r^0` |
Due to the point source light propagates in all directions symmetrically and hence, wavefront will be spherical as shown in the diagram.
As intensity of the source will be `I oo 1/r^2`
Where r is radius of the wavefront at any time.
Hence the intensity decreases in proportion to the distance squared.
APPEARS IN
RELATED QUESTIONS
Explain the construction of plane wavefront using Huygens’ principle.
What is the shape of the wavefront in the following case?
The portion of the wavefront of light from a distant star was intercepted by the Earth.
Using Huygens’ principle, verify the laws of reflection at a plane surface.
Use Huygens’s principle to explain the formation of diffraction pattern due to a single slit illuminated by a monochromatic source of light.
Define the term wavefront. Using Huygen’s wave theory, verify the law of reflection.
Relation between ray and wavefront is ______.
What is the phase difference between any two points lying on the same?
Two light beams of intensities in the ratio of 9 : 4 are allowed to interfere. The ratio of the intensity of maxima and minima ______.
Using Huygen's wave theory of light, show that the angle of incidence is equal to the angle of reflection. Draw a neat and labelled diagram.
Represent diagrammatically how the incident planar wavefronts of wavelength λ pass through an aperture of size d, when d is approximately equal to λ.
