Advertisements
Advertisements
Question
For paraxial rays, show that the focal length of a spherical mirror is one-half of its radius of curvature.
Solution
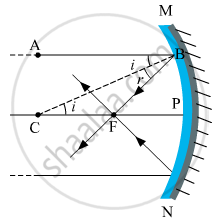
Consider a ray of light AB, parallel to the principal axis and incident on a spherical mirror at point B. The normal to the surface at point B is CB and CP = CB = R is the radius of curvature. The ray AB, after reflection from the mirror, will pass through F (concave mirror) or will appear to diverge from F (convex mirror) and obeys the law of reflection i.e. i = r.
From the geometry of the figure,
In Δ∆CFB,∠BCP =∠ABC = i (Alternate angles)
∠CBF = r
BF = FC (because i = r)
If the aperture of the mirror is small, B lies close to P, and therefore BF = PF
Or FC = FP = PF
Or PC = PF + FC = PF + PF
Or R = 2 PF = 2f
Or `"f" = "R"/2`
A similar relation holds for convex mirror also. In deriving this relation, we have assumed that the aperture of the mirror is small.
APPEARS IN
RELATED QUESTIONS
The rays of different colours fail to converge at a point after going through a converging lens. This defect is called
A cylindrical vessel of diameter 12 cm contains 800π cm3 of water. A cylindrical glass piece of diameter 8.0 cm and height 8.0 cm is placed in the vessel. If the bottom of the vessel under the glass piece is seen by the paraxial rays (see figure), locate its image. The index of refraction of glass is 1.50 and that of water is 1.33.

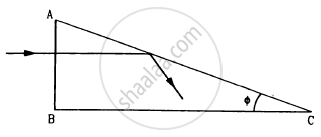
A light ray is incident normally on the face AB of a right-angled prism ABC (μ = 1.50) as shown in figure. What is the largest angle ϕ for which the light ray is totally reflected at the surface AC?
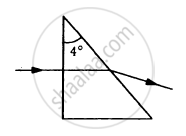
Find the angle of deviation suffered by the light ray shown in figure. The refractive index μ = 1.5 for the prism material.
A parallel beam of light is allowed to fall on a transparent spherical globe of diameter 30cm and refractive index 1.5. The distance from the centre of the globe at which the beam of light can converge is ______ mm.
The focal length f is related to the radius of curvature r of the spherical convex mirror by ______.
When a clock is viewed in a mirror, the needles exhibit a time which appears to be 8:20. Then the actual time will be:
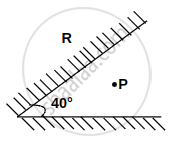
Two plane mirrors are inclined at an angle of 40°. The possible number of images of an object placed at point P would be?
A point object is placed at a distance of 30 cm from a convex mirror of a focal length of 30 cm. What is the separation between the image and the object?
A convex lens of focal length 15 cm is placed coaxially in front of a convex mirror. The lens is 5 cm from the pole of the mirror. When an object is placed on the axis at a distance of 20 cm from the lens, it is found that the image coincides with the object. Calculate the radius of curvature of the mirror - (consider all-optical event):
