Advertisements
Advertisements
Question
A cylindrical vessel of diameter 12 cm contains 800π cm3 of water. A cylindrical glass piece of diameter 8.0 cm and height 8.0 cm is placed in the vessel. If the bottom of the vessel under the glass piece is seen by the paraxial rays (see figure), locate its image. The index of refraction of glass is 1.50 and that of water is 1.33.

Solution
Given,
Diameter of the cylindrical vessel = 12 cm
∴ radius r = 6 cm
Diameter of the cylindrical glass piece = 8 cm
∴ radius r' = 4 cm and its height, h1 = 8 cm
Refractive index of glass, μg = 1.5
Refractive index of water, μw = 1.3
Let h be the final height of the water column.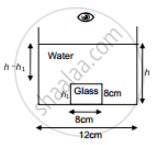
The volume of the cylindrical water column after the glass piece is put will be:
\[\pi\] r2h = 800π +
\[\pi\] r'2h1
or r2h = 800 + r'2h1
or (6)2 h = 800 + (4)2 8
\[or `h = \frac{800 + 128} ( 36 ) = 928/36 = 25.7 cm`
There will be two shifts; due to the glass block as well as water:
\[∆ t_1 = \left[ 1 - \frac{1}{\mu_g} \right] t_g = \left[ 1 - \frac{1}{\frac{3}{2}} \right] \times 8 = 2 . 26 cm\]
\[ ∆ t_2 = \left[ 1 - \frac{1}{\mu_w} \right] t_w = \left[ 1 - \frac{1}{\frac{4}{3}} \right] \times \left( 25 . 7 - 8 \right) = 4 . 44 cm\]
Hence, the total shift = (Δt1+ Δt2) = (2.66 + 4.44) cm = 7.1 cm above the bottom.
APPEARS IN
RELATED QUESTIONS
Calculate the distance of an object of height h from a concave mirror of radius of curvature 20 cm, so as to obtain a real image of magnification 2. Find the location of the image also.
a) Give two reasons to explain why reflecting telescopes are preferred over refracting type.
Use the mirror equation to show that an object placed between f and 2f of a concave mirror produces a real image beyond 2f.
Using mirror formula, explain why does a convex mirror always produce a virtual image.
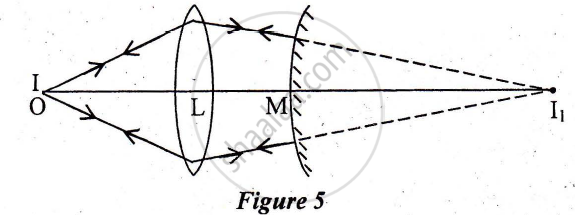
A point object O is placed at a distance of 15cm from a convex lens L of focal length 1 Ocm as shown in Figure 5 below. On the other side of the lens, a convex mirror M is placed such that its distance from the lens is equal to the focal length of the lens. The final image formed by this combination is observed to coincide with the object O. Find the focal length of the convex mirror
Use the mirror equation to show a convex mirror always produces a virtual image independent of the location of the object ?
Can a plane mirror ever form a real image?
following Figure shows two rays A and B being reflected by a mirror and going as A' and B'. The mirror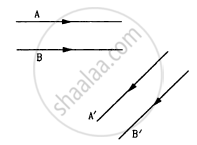
Mark the correct options.
Which of the following (referred to a spherical mirror) do (does) not depend on whether the rays are paraxial or not?
(a) Pole
(b) Focus
(c) Radius of curvature
(d) Principal axis
A small object is placed at the centre of the bottom of a cylindrical vessel of radius 3 cm and height 4 cm filled completely with water. Consider the ray leaving the vessel through a corner. Suppose this ray and the ray along the axis of the vessel are used to trace the image. Find the apparent depth of the image and the ratio of real depth to the apparent depth under the assumptions taken. Refractive index of water = 1.33.
A light ray is incident at an angle of 45° with the normal to a √2 cm thick plate (μ = 2.0). Find the shift in the path of the light as it emerges out from the plate.
Find the maximum angle of refraction when a light ray is refracted from glass (μ = 1.50) to air.
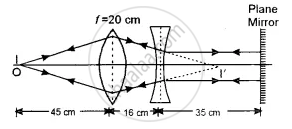
The figure below shows the positions of a point object O, two lenses, a plane mirror and the final image I which coincides with the object. The focal length of the convex lens is 20 cm. Calculate the focal length of the concave lens.
Car B overtakes car A at a relative speed of 40 ms-1. How fast will the image of car B appear to move in the mirror of focal length 10 cm fitted in car A, when car B is 1.9 m away from car A?
When a clock is viewed in a mirror, the needles exhibit a time which appears to be 8:20. Then the actual time will be:
A point object is placed at a distance of 30 cm from a convex mirror of a focal length of 30 cm. What is the separation between the image and the object?
