Advertisements
Advertisements
Question
For the circuit shown in the diagram below:

What is the value of:
(i) current through 6 Ω resistor?
(ii) potential difference across 12 Ω resistor?
Solution
The resistors of 6 Ω and 3 Ω are connected in series. Therefore, their net resistance can be calculated as:
R = R1 + R2
Here, R1 = 6 Ω
R2 = 3 Ω
So:
R = 6 Ω + 3 Ω = 9 Ω
The current through this branch, I = V/R
I = 4/9 = 0.44 A
In a series combination, the current remains the same. So the current through the 6 Ω resistor is 0.44 A.
(2) The current through the branch with resistors of 12 Ω and 3 Ω:
I = V/R
I = 4/(12 + 3) = 4 / 15 A
The potential difference across the 12 Ω resistance can be obtained by using the equation,
V = IR.
V = (4 / 15) x 12 = 3.2 V
APPEARS IN
RELATED QUESTIONS
You have three resistors of values 2Ω, 3Ω and 5Ω. How will you join them so that the total resistance is more than 7Ω?
1) Draw a diagram for the arrangement
2) Calculate the equivalent resistance.
What is the SI unit of potential difference?
What p.d. is needed to send a current of 6 A through an electrical appliance having a resistance of 40 Ω?
In the circuit diagram given below, the current flowing across 5 ohm resistor is 1 amp. Find the current flowing through the other two resistors.
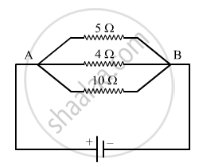
In the circuit shown below:

The potential difference across the 3 Ω resistor is:
Explain the statement ‘the potential difference between two points is 1 volt’.
What would you suggest to a student if while performing an experiment he finds that the pointer/needle of the ammeter and voltmeter do not coincide with the zero marks on the scales when the circuit is open? No extra ammeter/voltmeter is available in the laboratory.
Find the resistance of a conductor if the electric current flowing through it is 0.35 A when the potential difference across it is 1.4 V.
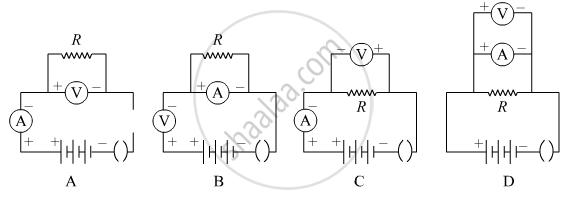
Which one of the following is the correct set-up for studying the dependence of the current on the potential difference across a resistor and why?
An electric charge always flows from a point at a ______ to a point at a ______.
