Advertisements
Advertisements
Question
If 1is a zero of the quadratic polynomial `ax^2 – 3(a – 1)x – 1`is 1, then find the value of a.
Solution
Given: x = 1 is one zero of the polynomial `ax^2 – 3(a – 1) x – 1`
Therefore, it will satisfy the above polynomial.
Now, we have
`a(1)^2 – (a – 1)1 – 1 = 0`
`⇒ a – 3a + 3 – 1 = 0`
`⇒ –2a = – 2`
`⇒ a = 1`
APPEARS IN
RELATED QUESTIONS
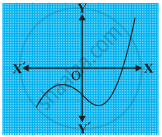
The graphs of y = p(x) are given in following figure, for some polynomials p(x). Find the number of zeroes of p(x).
If 3 is a zero of the polynomial `2x^2 + x + k`, find the value of k.
If -4 is a zero of the polynomial `x^2 – x – (2k + 2) is –4`, then find the value of k.
If -2 is a zero of the polynomial `3x^2 + 4x + 2k` then find the value of k.
Given that one of the zeroes of the cubic polynomial ax3 + bx2 + cx + d is zero, the product of the other two zeroes is ______.
If the zeroes of the quadratic polynomial ax² + bx + c, c # 0 are equal, then ______.
If one of the zeroes of a quadratic polynomial of the form x² + ax + b is the negative of the other, then it ______.
If x4 + 3x2 + 7 is divided by 3x + 5, then the possible degrees of quotient and remainder are ______.
If p(x) is a polynomial of at least degree one and p(k) = 0, then k is known as ______.
The number of quadratic polynomials having zeroes –5 and –3 is ______.
