Advertisements
Advertisements
प्रश्न
If 1is a zero of the quadratic polynomial `ax^2 – 3(a – 1)x – 1`is 1, then find the value of a.
उत्तर
Given: x = 1 is one zero of the polynomial `ax^2 – 3(a – 1) x – 1`
Therefore, it will satisfy the above polynomial.
Now, we have
`a(1)^2 – (a – 1)1 – 1 = 0`
`⇒ a – 3a + 3 – 1 = 0`
`⇒ –2a = – 2`
`⇒ a = 1`
APPEARS IN
संबंधित प्रश्न
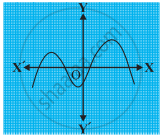
The graphs of y = p(x) are given in following figure, for some polynomials p(x). Find the number of zeroes of p(x).
Find the zeros of the polynomial `f(x) = x^2 + 7x + 12` and verify the relation between its zeroes and coefficients.
If one zero of the polynomial `x^2-4x+1 is (2+sqrt3)` , write the other zero.
Find ∝ , β are the zeros of polynomial ∝ +β= 6 and ∝β 4 then write the polynomial.
If -2 is a zero of the polynomial `3x^2 + 4x + 2k` then find the value of k.
If ∝ and β are the zeros of the polynomial f(x) = `6x^2 + x - 2 `find the value of `(∝/β+∝/β) `
If x3 + 1 is divided by x2 + 5, then the possible degree of quotient is ______.
The zeroes of the quadratic polynomial x2 + kx + k, k ≠ 0 ______.
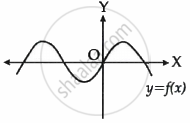
The graph of y = f(x) is shown in the figure for some polynomial f(x). The number of zeroes of f(x) are ______.
If α and β are the zeroes of the polynomial x2 + x − 2, then find the value of `alpha/beta+beta/alpha`
