Advertisements
Advertisements
Question
If α and β are the zeros of the polynomial f(x) = x2 + px + q, then a polynomial having \[\frac{1}{\alpha} \text{and}\frac{1}{\beta}\] is its zero is
Options
x2 + qx + p
x2 − px + q
qx2 + px + 1
px2 + qx + 1
Solution
Let `alpha` and `beta` be the zeros of the polynomial f(x) = x2 + px + q,.Then,
`alpha + ß = - (text{coefficient of x})/(text{coefficient of } x^2)`
`= -p/1`
`=-p`
`alpha ß = (\text{constat term})/(text{coefficient of} x^2)`
`= q/1`
`= q`
Let S and R denote respectively the sum and product of the zeros of a polynomial
Whose zeros are `1/alpha` and `1/beta` .then
`s = 1/alpha + 1/beta`
`=(alpha + beta)/(alpha beta)`
`= (-p)/q`
` R = 1/alpha xx1/beta`
`=1/(alpha beta)`
`= 1/q`
Hence, the required polynomial `g(x)` whose sum and product of zeros are S and R is given by
`x^2 - Sx + R = 0`
`x^2 + p/qx+ 1/q =0`
`(qx^2+px+1)/q=0`
`⇒ qx^2 + px + 1`
So `g(x) = qx^2 + px + 1`
Hence, the correct choice is `(C)`
APPEARS IN
RELATED QUESTIONS
Write the standard form of a cubic polynomial with real coefficients.
The sum and product of the zeros of a quadratic polynomial are \[- \frac{1}{2}\] and −3 respectively. What is the quadratic polynomial.
If x = 1 is a zero of the polynomial f(x) = x3 − 2x2 + 4x + k, write the value of k.
State whether the given algebraic expression are polynomial? Justify.
`y + 1/y`
Divide. Write the quotient and the remainder.
(5x3 − 3x2) ÷ x2
Let the polynomials be
(A) −13q5 + 4q2 + 12q
(B) (x2 + 4)(x2 + 9)
(C) 4q8 – q6 + q2
(D) `– 5/7 y^12 + y^3 + y^5`
Then ascending order of their degree is
Which of the following is not the graph of quadratic polynomial?
An asana is a body posture, originally and still a general term for a sitting meditation pose, and later extended in hatha yoga and modern yoga as exercise, to any type of pose or position, adding reclining, standing, inverted, twisting, and balancing poses. In the figure, one can observe that poses can be related to representation of quadratic polynomial.


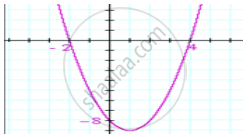
In the graph, how many zeroes are there for the polynomial?
Basketball and soccer are played with a spherical ball. Even though an athlete dribbles the ball in both sports, a basketball player uses his hands and a soccer player uses his feet. Usually, soccer is played outdoors on a large field and basketball is played indoor on a court made out of wood. The projectile (path traced) of soccer ball and basketball are in the form of parabola representing quadratic polynomial.

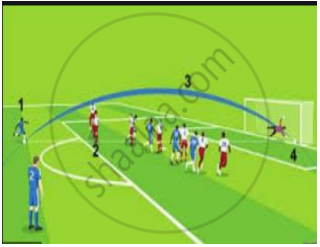
The shape of the path traced shown is:
Classify the following as a constant, linear, quadratic and cubic polynomials:
t2
