Advertisements
Advertisements
Question
If f(x) = `x^4– 5x + 6" is divided by g(x) "= 2 – x2`
Solution
`f(x) as x^4 + 0x^3 + 0x^2 – 5x + 6 and g(x) as – x^2 + 2`
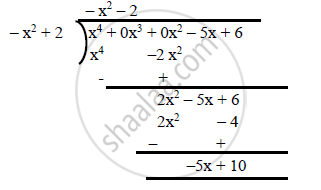
Quotient q(x) = `– x^2 – 2`
Remainder r(x) = –5x + 10
APPEARS IN
RELATED QUESTIONS
Find the zeros of the quadratic polynomial 9x2 - 5 and verify the relation between the zeros and its coefficients.
Verify that the numbers given along side of the cubic polynomials are their zeroes. Also verify the relationship between the zeroes and the coefficients.
`2x^3 + x^2 – 5x + 2 ; 1/2, 1, – 2`
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients
`f(x)=x^2-(sqrt3+1)x+sqrt3`
If α and β are the zeros of the quadratic polynomial f(x) = 6x2 + x − 2, find the value of `alpha/beta+beta/alpha`.
If the sum of the zeros of the quadratic polynomial f(t) = kt2 + 2t + 3k is equal to their product, find the value of k.
If α and β are the zeros of the quadratic polynomial f(x) = x2 − p (x + 1) — c, show that (α + 1)(β +1) = 1− c.
If α, β, γ are the zeros of the polynomial f(x) = ax3 + bx2 + cx + d, then α2 + β2 + γ2 =
If two of the zeros of the cubic polynomial ax3 + bx2 + cx + d are each equal to zero, then the third zero is
If two zeros x3 + x2 − 5x − 5 are \[\sqrt{5}\ \text{and} - \sqrt{5}\], then its third zero is
Given that one of the zeroes of the cubic polynomial ax3 + bx2 + cx + d is zero, the product of the other two zeroes is ______.
