Advertisements
Advertisements
प्रश्न
If f(x) = `x^4– 5x + 6" is divided by g(x) "= 2 – x2`
उत्तर
`f(x) as x^4 + 0x^3 + 0x^2 – 5x + 6 and g(x) as – x^2 + 2`
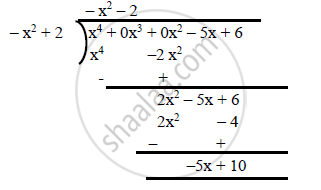
Quotient q(x) = `– x^2 – 2`
Remainder r(x) = –5x + 10
APPEARS IN
संबंधित प्रश्न
if α and β are the zeros of ax2 + bx + c, a ≠ 0 then verify the relation between zeros and its cofficients
If 𝛼 and 𝛽 are the zeros of the quadratic polynomial p(x) = 4x2 − 5x −1, find the value of α2β + αβ2.
If α and β are the zeros of the quadratic polynomial f(x) = x2 − px + q, prove that `alpha^2/beta^2+beta^2/alpha^2=p^4/q^2-(4p^2)/q+2`
If If α and β are the zeros of the quadratic polynomial f(x) = x2 – 2x + 3, find a polynomial whose roots are α + 2, β + 2.
If If α and β are the zeros of the quadratic polynomial f(x) = x2 – 2x + 3, find a polynomial whose roots are `(alpha-1)/(alpha+1)` , `(beta-1)/(beta+1)`
If all the zeroes of a cubic polynomial are negative, then all the coefficients and the constant term of the polynomial have the same sign.
Find the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials:
3x2 + 4x – 4
Given that `sqrt(2)` is a zero of the cubic polynomial `6x^3 + sqrt(2)x^2 - 10x - 4sqrt(2)`, find its other two zeroes.
Find the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials:
`v^2 + 4sqrt(3)v - 15`
If α, β are zeroes of quadratic polynomial 5x2 + 5x + 1, find the value of α2 + β2.
